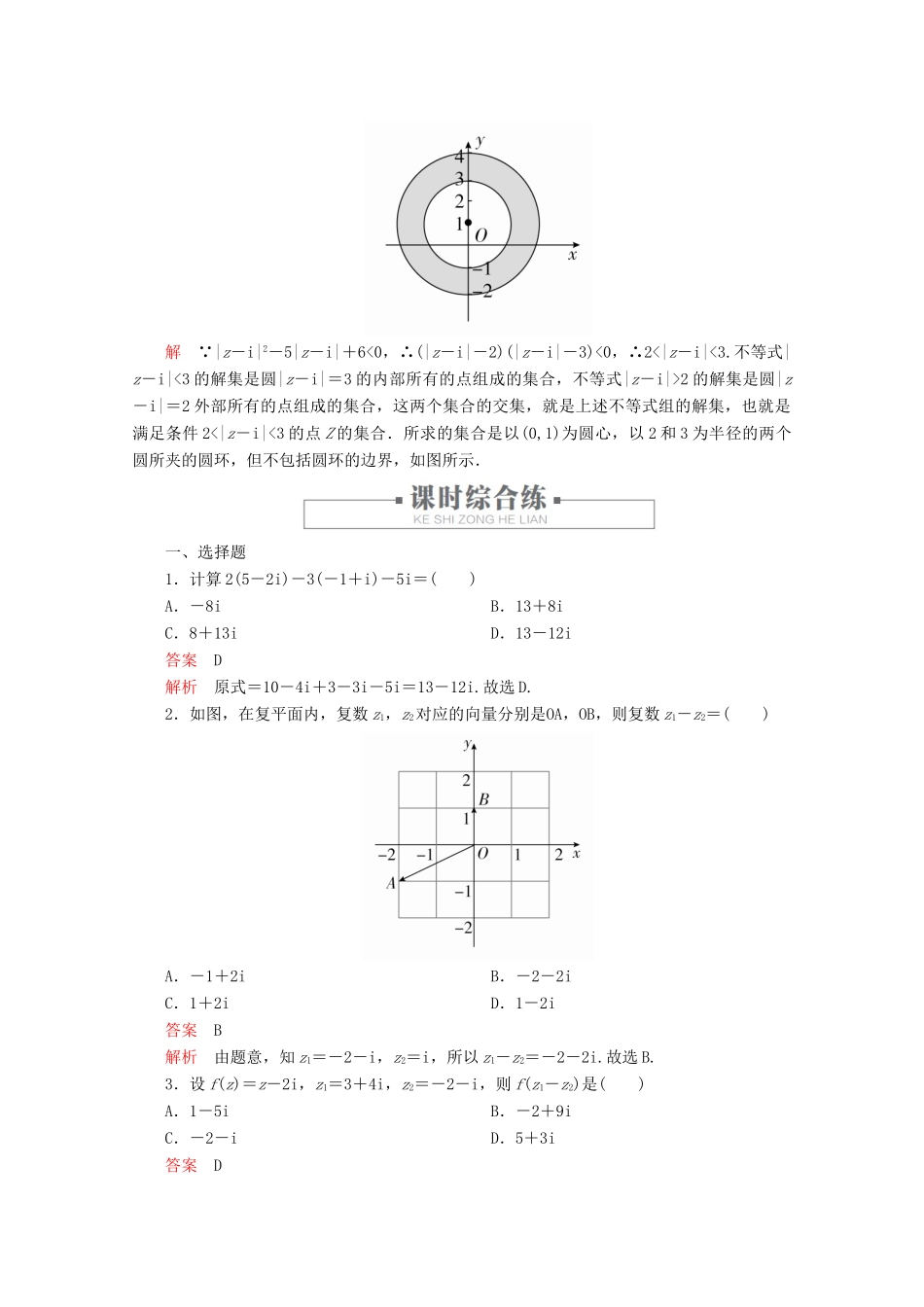
课时作业18复数的加、减运算及其几何意义知识点一复数的加减运算1.已知复数z1=1+3i,z2=3+i(i为虚数单位).在复平面内,z1-z2对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限答案B解析 z1=1+3i,z2=3+i,∴z1-z2=-2+2i,故z1-z2在复平面内对应的点(-2,2)在第二象限.2.设z1=1-i,z2=a+2ai(a∈R),其中i是虚数单位,若复数z1+z2是纯虚数,则有()A.a=1B.a=C.a=0D.a=-1答案D解析 复数z1+z2=1-i+a+2ai=1+a+(2a-1)i是纯虚数,∴a+1=0,2a-1≠0,∴a=-1.知识点二复数加减运算的几何意义3.在复平面上复数-1+i,0,3+2i所对应的点分别是A,B,C,则平行四边形ABCD的对角线BD的长为()A.5B.C.D.答案B解析BA对应的复数为-1+i,BC对应的复数为3+2i, BD=BA+BC,∴BD对应的复数为(-1+i)+(3+2i)=2+3i.∴BD的长为.4.已知复数z1对应的向量的终点在第二象限,复数z2对应的向量的终点在第二象限,那么复数z1+z2对应的向量的终点在()A.第一象限B.第二象限C.第三象限D.第四象限答案B解析根据题意结合向量加法运算的平行四边形法则知复数z1+z2对应的向量的终点一定在复数z1,z2对应的向量所在的直线之间,即其终点也是在第二象限.故选B.5.满足条件|z-2i|+|z+1|=的点的集合是()A.正方形B.直线C.线段D.圆答案C解析|z-2i|+|z+1|=表示动点Z到两定点(0,2)与(-1,0)的距离之和为常数,又点(0,2)与(-1,0)之间的距离为,所以动点的集合为以两定点(0,2)与(-1,0)为端点的线段.故选C.6.已知z1,z2∈C,|z1+z2|=2,|z1|=2,|z2|=2,则|z1-z2|为________.答案2解析由复数加法、减法的几何意义知,以复平面上对应z1,z2的向量为邻边的平行四边形为正方形,所以|z1-z2|=2.知识点三复数加减运算几何意义的应用7.△ABC的三个顶点所对应的复数分别为z1,z2,z3,复数z满足|z-z1|=|z-z2|=|z-z3|,则z对应的点是△ABC的()A.外心B.内心C.重心D.垂心答案A解析由复数模及复数减法运算的几何意义,结合条件可知复数z的对应点P到△ABC的顶点A,B,C距离相等,∴P为△ABC的外心.8.复平面上三点A,B,C分别对应复数1,2i,5+2i,则由A,B,C所构成的三角形是()A.直角三角形B.等腰三角形C.锐角三角形D.钝角三角形答案A解析|AB|=|2i-1|=,|AC|=|4+2i|=,|BC|=5,∴|BC|2=|AB|2+|AC|2.故选A.9.若复数z满足|z|=2,则|1+i+z|的取值范围是()A.[1,3]B.[1,4]C.[0,3]D.[0,4]答案D解析复数z对应的点Z(a,b)的轨迹为以原点为圆心、2为半径的圆,|1+i+z|表示点Z(a,b)到点M(-1,-)的距离.因为(-1,-)在|z|=2这个圆上,所以距离最小是0,最大是4.故所求取值范围是[0,4].10.设z∈C,在复平面内z对应的点为Z,那么满足|z-i|2-5|z-i|+6<0的点Z的集合是什么图形?解 |z-i|2-5|z-i|+6<0,∴(|z-i|-2)(|z-i|-3)<0,∴2<|z-i|<3.不等式|z-i|<3的解集是圆|z-i|=3的内部所有的点组成的集合,不等式|z-i|>2的解集是圆|z-i|=2外部所有的点组成的集合,这两个集合的交集,就是上述不等式组的解集,也就是满足条件2<|z-i|<3的点Z的集合.所求的集合是以(0,1)为圆心,以2和3为半径的两个圆所夹的圆环,但不包括圆环的边界,如图所示.一、选择题1.计算2(5-2i)-3(-1+i)-5i=()A.-8iB.13+8iC.8+13iD.13-12i答案D解析原式=10-4i+3-3i-5i=13-12i.故选D.2.如图,在复平面内,复数z1,z2对应的向量分别是OA,OB,则复数z1-z2=()A.-1+2iB.-2-2iC.1+2iD.1-2i答案B解析由题意,知z1=-2-i,z2=i,所以z1-z2=-2-2i.故选B.3.设f(z)=z-2i,z1=3+4i,z2=-2-i,则f(z1-z2)是()A.1-5iB.-2+9iC.-2-iD.5+3i答案D解析 f(z)=z-2i,∴f(z1-z2)=z1-z2-2i=(3+4i)-(-2-i)-2i=(3+2)+(4+1-2)i=5+3i.4.复平面内点A,B,C对应的复数分别为i,1,4+2i,由A→B→C→D按逆时针顺序作平行四边形ABCD,则|BD|等于()A.5B.C.D.答案B解析依据复数加法、减法的几何意义可得BA=(-1,1),BC=(3,2),所以BD=BA+BC=(2,3),所以|BD|=|...