高一数学函数的性质（1）——单调性苏教版知识精讲VIP免费

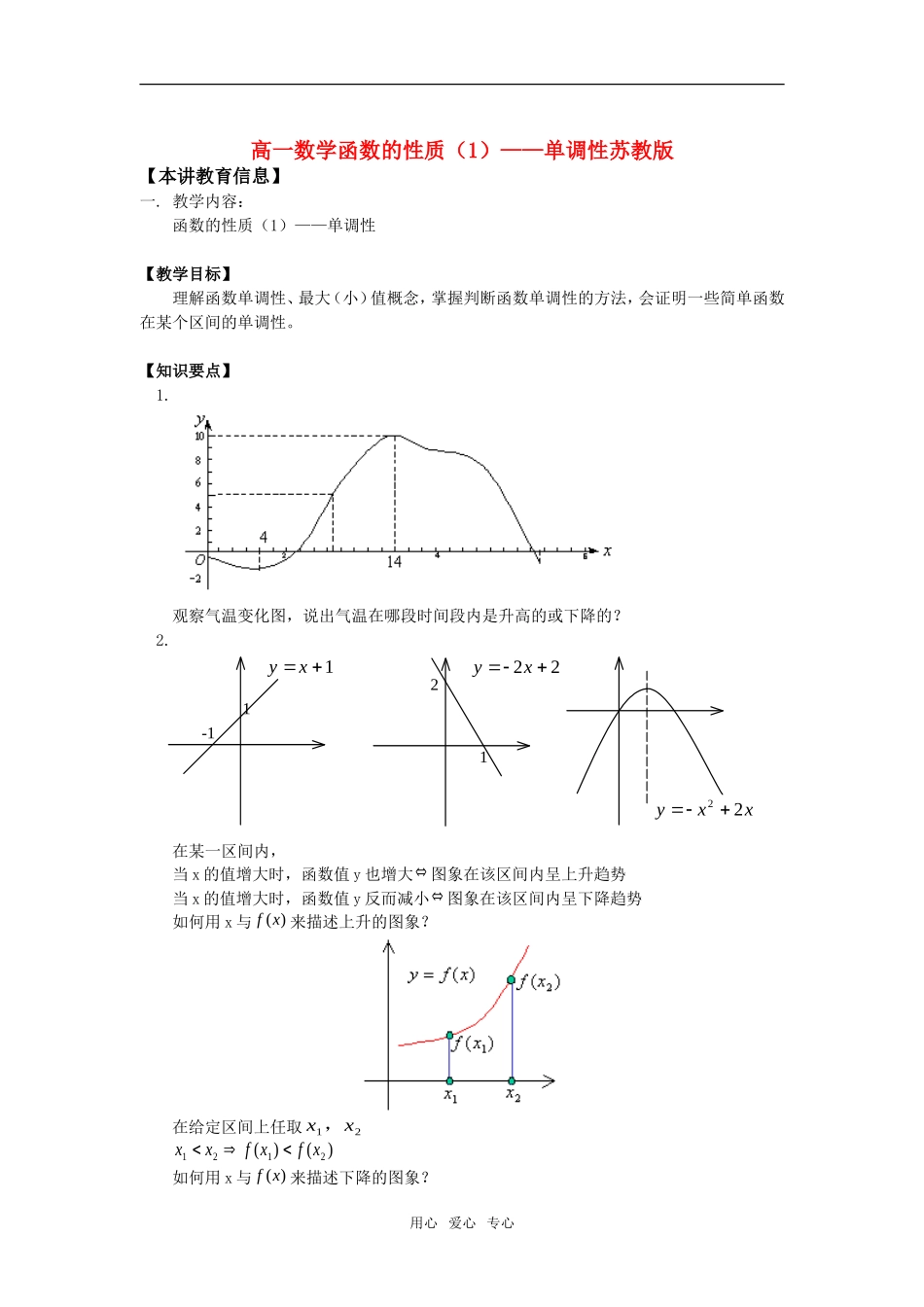
高一数学函数的性质（1）——单调性苏教版【本讲教育信息】一.教学内容：函数的性质（1）——单调性【教学目标】理解函数单调性、最大（小）值概念，掌握判断函数单调性的方法，会证明一些简单函数在某个区间的单调性。【知识要点】1.观察气温变化图，说出气温在哪段时间段内是升高的或下降的？2.21-11yx1yx22yxx22在某一区间内，当x的值增大时，函数值y也增大图象在该区间内呈上升趋势当x的值增大时，函数值y反而减小图象在该区间内呈下降趋势如何用x与fx()来描述上升的图象？在给定区间上任取xx12，xxfxfx1212()()如何用x与fx()来描述下降的图象？用心爱心专心在给定区间上任取xx12，xxfxfx1212()()［定义］1.一般地，设函数yfx()定义域为A，区间IA。如果对于区间I内的任意两个值xx12，，当xx12时，都有fxfx()()12，那么就说yfx()在区间I上是单调递增函数，I称为yfx()单调递增区间。如果对于区间I内的任意两个值xx12，，当xx12时，都有fxfx()()12，那么就说yfx()在区间I上是单调递减函数，I称为yfx()单调递减区间。2.一般地，设yfx()的定义域为A，若存在定值xA0，使得对于任意xA，有fxfx()()0恒成立，则称fx()0为yfx()的最大值。若存在定值xA0，使得对于任意xA，有fxfx()()0恒成立，则称fx()0为yfx()的最小值。［思考］1.（1）若函数yfx()在R上单调递增，比较f()1与f()2的大小。（2）若函数yfx()在11，上单调递增，则（a）比较f12与f()1的大小；（b）对于任意的x11，，fx()与f()1？2.（1）已知yfx()在R上单调递减且faf()()1，求a的范围。变：若fxfx()()21，求x的取值范围。【典型例题】例1.证明函数fxx()32在R上是增函数。证明：（1）取值设xx12，是R上的任意两个实数，且xx12，则（2）作差fxfxxxxx()()12121232323（3）判断由xx12，得：xx120于是fxfx120（4）结论所以，fxx()32在R上是增函数。用心爱心专心例2.判断函数yxx10的单调性，并写出单调区间。解：此函数定义域为，，00首先画出函数yx1的图象yOx从图象上观察，我们可知，函数yx1在，0和0，上均为单调递减。∴函数yx1的单调减区间为，0和0，注意：我们能说函数yx1在整个定义域内单调递减吗？为什么？例3.求证：函数fxx()11在区间，0上是单调增函数。证明：（1）取值设xx12，是，0上的任意两个实数，且xx12，则（2）作差fxfxxxxxxxxx1212211212111111（3）判断xxxx121200，又xxxx121200，，，fxfxxxxxfxfx121212120（4）结论所以fxx()11在区间，0上是单调增函数。例4.如图，定义在闭区间66，上的函数yfx()的图象，根据图象说出yfx()的最大值、最小值及单调区间。用心爱心专心解：函数yfx()的单调减区间为63，和03，，以及56，函数yfx()的单调增区间为30，和35，最大值为f()6，最小值为f()3例5.已知函数yfx()的定义域是abacb，，。当xac，时，fx()是单调增函数；当xcb，时，fx()是单调减函数。试证明fx()在xc时取得最大值。证明：因为当xac，时，fx()是单调增函数所以对于任意xac，都有fxfc()()又因为当xcb，时，fx()是单调减函数所以对于任意的xcb，都有fxfc()()因此，对于任意xab，都有fxfc()()即在xc时取得最大值。【模拟试题】一.选择题。1.已知fx()在0，上为增函数，则fff()()()23，，的大小顺序是（）A.fff()()()32B.fff()()()23C.fff()()()23D.fff()()()322.已知函数fxxax()2212在区间，4上是减函数，则实数a的取值范围是（）A.a3B.a3C.a3D.a53.下列函数中，在区间1，上为减函数的是（）A.yx2B.yxx223C.y...