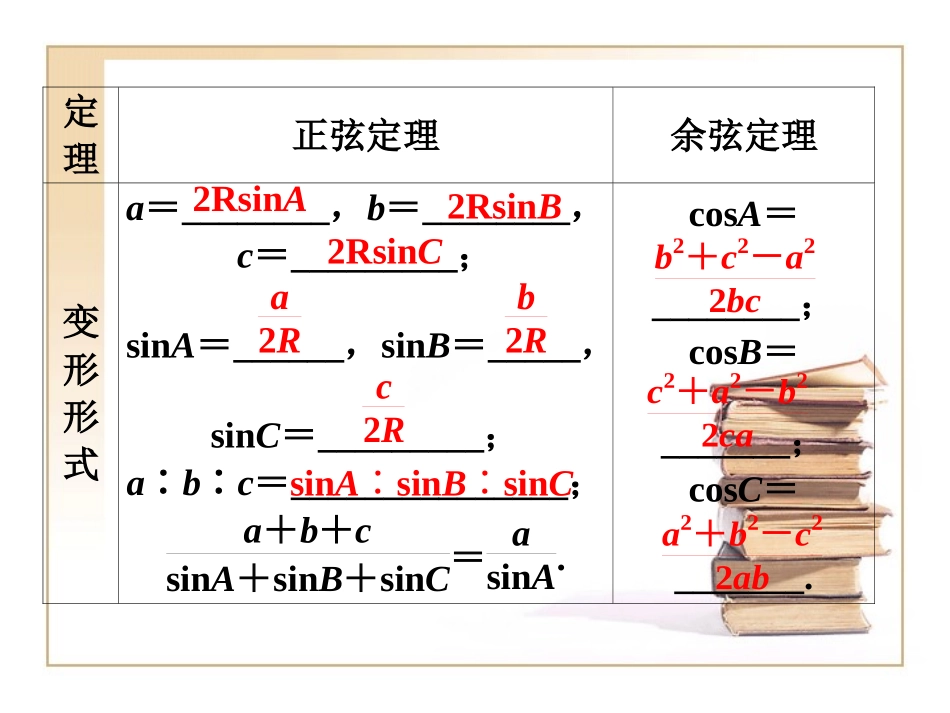
正弦定理和余弦定理定理正弦定理余弦定理内容asinA=bsinB=csinC=2R(R为△ABC外接圆半径)a2=_______________;b2=_______________;c2=________________.b2+c2-2bccosAc2+a2-2cacosBa2+b2-2abcosC基础梳理基础梳理定理正弦定理余弦定理变形形式a=________,b=________,c=_________;sinA=______,sinB=_____,sinC=_________;a∶b∶c=_______________;a+b+csinA+sinB+sinC=asinA.cosA=________;cosB=_______;cosC=_______.2RsinA2RsinB2RsinCa2Rb2Rc2RsinAsin∶Bsin∶Cb2+c2-a22bcc2+a2-b22caa2+b2-c22ab练习.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(2b-c)·cosA-acosC=0.(1)求角A的大小;(2)若a=3,S△ABC=334,试判断△ABC的形状,并说明理由.解:(1)法一: (2b-c)cosA-acosC=0,由正弦定理得,(2sinB-sinC)cosA-sinAcosC=0,∴2sinBcosA-sin(A+C)=0,即sinB(2cosA-1)=0. 0