正弦定理 ()VIP免费

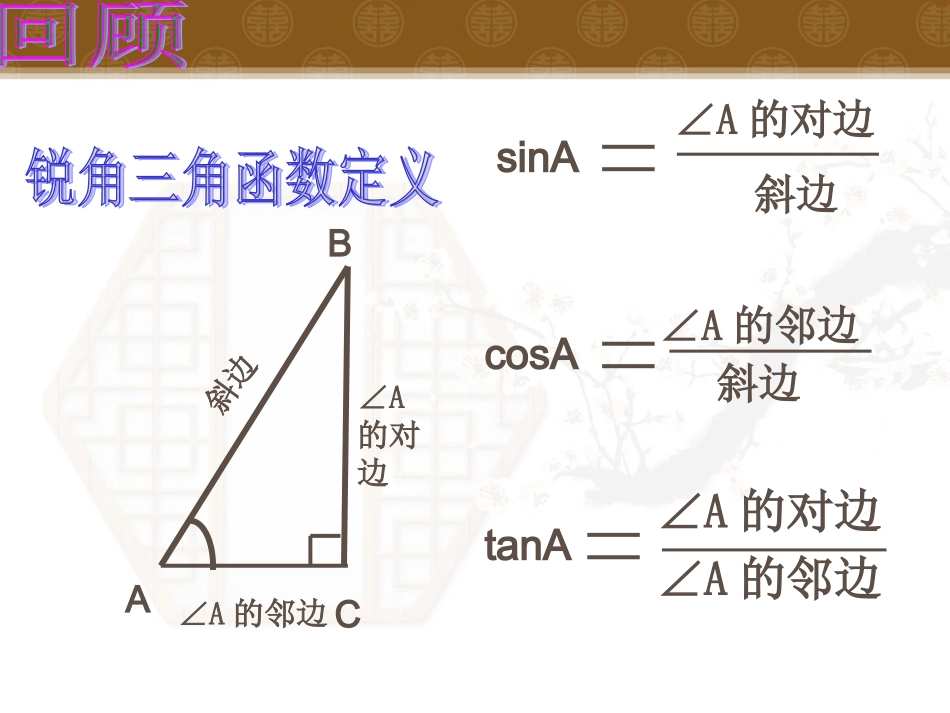
特殊角的三角函数值表0030045060090021三角函数三角函数值角sincostan2122222323331310010不存在∠A的对边∠A的邻边tanAcosA∠A的邻边斜边∠A的对边sinA斜边ABC∠A的对边∠A的邻边斜边复习三角形中的边角关系1、角的关系2、边的关系3、边角关系180CBAcbacba,大角对大边（一）任意三角形中的边角关系（二）直角三角形中的边角关系（角C为直角）1、角的关系2、边的关系3、边角关系90BA222cba1.1.1正弦定理引入直角三角形中边与角的关系？cbaCBA1sin,sin,sinCcbBcaA问题：在任意三角形中，这一关系式是否成立？CccBbcAacsin,sin,sin===CcBbAasinsinsin==bADcADCBsin,sin所以AD=csinB=bsinC,即,sinsinCcBb同理可得,sinsinCcAaCcBbAasinsinsin即：DAcbCB过点A作ADBC⊥于D,此时有(1)若三角形是锐角三角形,如图学科网CCbADsinsin）（且CcBbAasinsinsin可得D(2)若三角形是钝角三角形,且角C是钝角此时也有cADBsin交BC延长线于D,过点A作ADBC⊥，CAcbB图2正弦定理在一个三角形中各边和它所对角的正弦的比相等.＝＝asinAbsinBcsinC＝?1CCABCC1abcO如图:RC1cCc2sinsinRAaRBb2sin2sin，同理：为外接圆半径即：RRCcBbAa2sinsinsin(3)外接圆法正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即RCcBbAa2sinsinsin一般的，把三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素。已知三角形的几个元素求其他元素的过程叫做解三角形。(1)a=2RsinA,b=2RsinB,c=2RsinC；(2)sinA:sinB:sinC=a:b:c；BacAbcCabSΔABCsin21sin21sin21)3(注意:1．在△ABC中，角A，B，C的对边分别是a，b，c，若A∶B∶C＝1∶2∶3，则a∶b∶c等于()A．1∶2∶3B．2∶3∶4C．3∶4∶5D．1∶∶23答案D正弦定理可以解决三角形中哪类问题：①已知两角和一边，求其他角和边.②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角.CcBbAasinsinsin例在△ABC中，已知c=10,A=45。,C=30。求a,b(精确到0.01）.解：且105C)(A180B∵CcBbsinsin∴b=CBcsinsin19.32=30sin105sin10CcAasinsin∵∴a=CAcsinsin14.14=21030sin45sin10BACbc)26(5a在中，已知，求.ABC45,24,4BbaA典型例题解：由BbAasinsin得21sinsinbBaA∵在中ABCba∴A为锐角30A∵a>b，∴A>B，B<60°∴B＝45°.故B＝30°或150°.由a>b，得A>B，∴B＝30°，故C＝90°，由勾股定理得c＝2.解：由正弦定理得：故B＝60°或120°.当B＝60°时，C＝90°，当B＝120°时，C＝30°，解析∵△ABC的外接圆直径为2R＝2，解析设三角形外接圆半径为R，则由πR2＝π，得R＝1，∴abc＝1.10．在△ABC中，已知a，b，c分别为内角A，B，C的对边，若b＝2a，B＝A＋60°，则A＝______.解析∵b＝2a∴sinB＝2sinA，又∵B＝A＋60°，∴sin(A＋60°)＝2sinA即sinAcos60°＋cosAsin60°＝2sinA，∴A＝30°.所以等式成立又0