高中数学空间线面关系的判定教案人教新课标必修2VIP免费

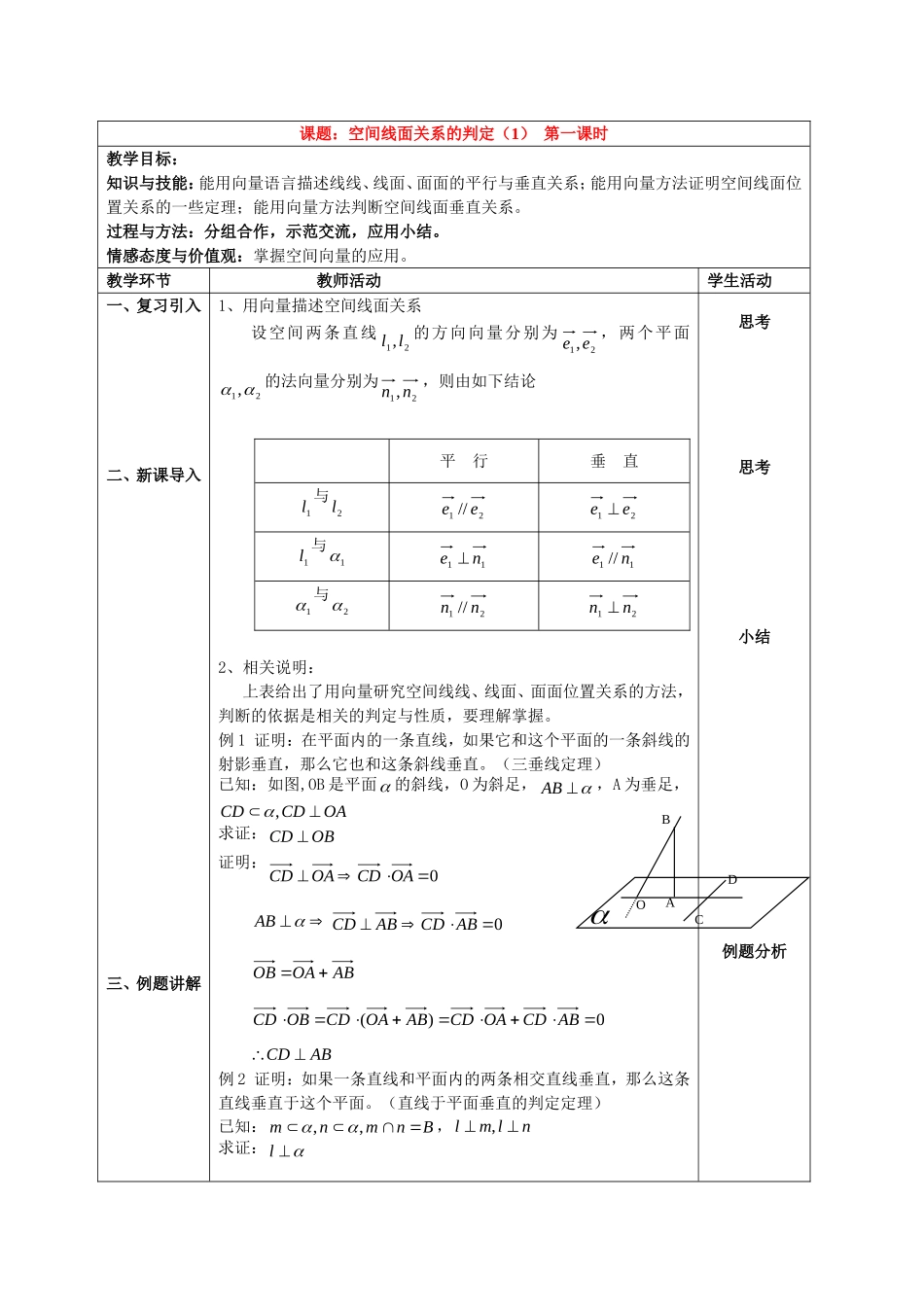
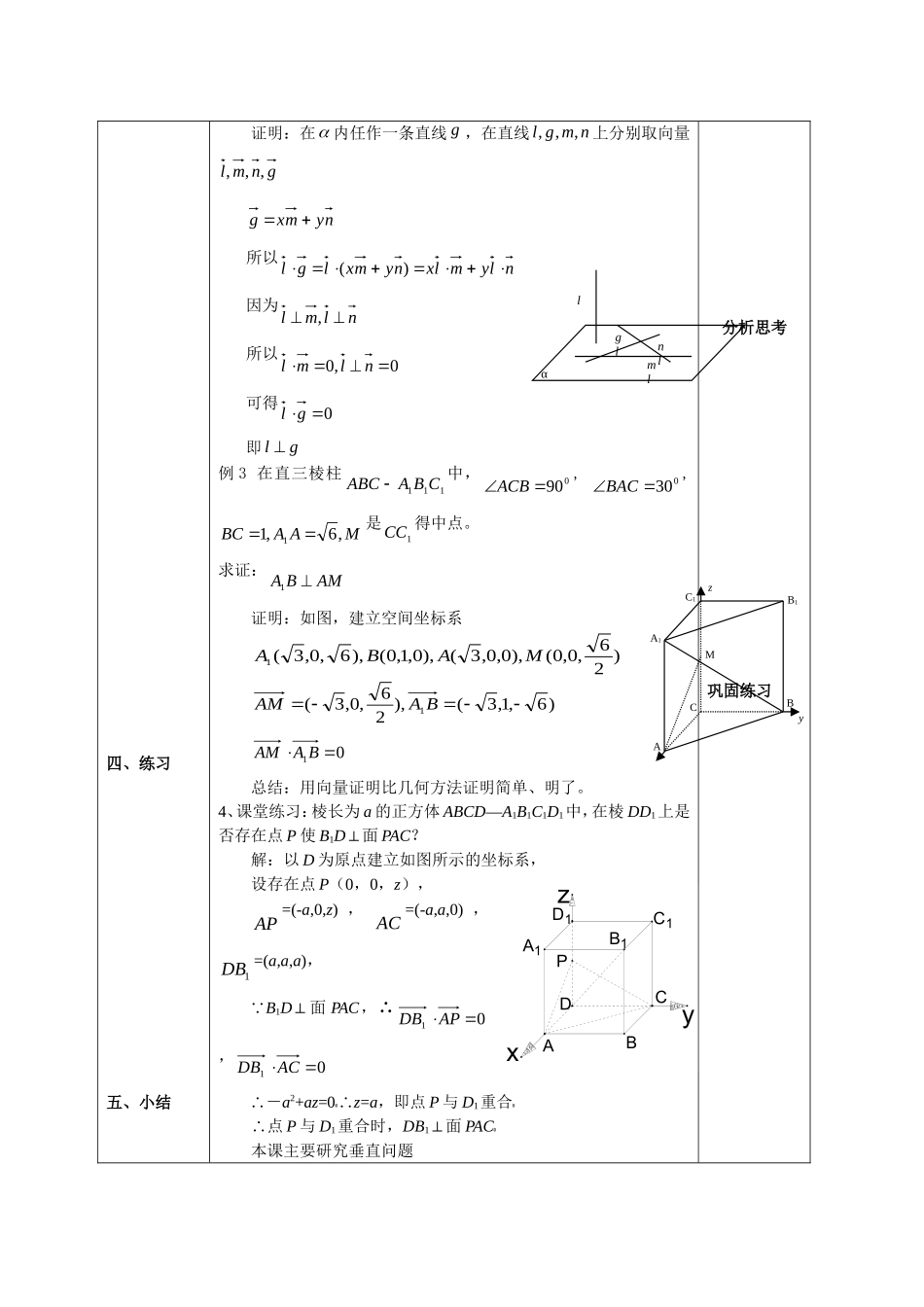
ABCDO课题：空间线面关系的判定（1）第一课时教学目标：知识与技能：能用向量语言描述线线、线面、面面的平行与垂直关系；能用向量方法证明空间线面位置关系的一些定理；能用向量方法判断空间线面垂直关系。过程与方法：分组合作，示范交流，应用小结。情感态度与价值观：掌握空间向量的应用。教学环节教师活动学生活动一、复习引入二、新课导入三、例题讲解1、用向量描述空间线面关系设空间两条直线21,ll的方向向量分别为21,ee，两个平面21,的法向量分别为21,nn，则由如下结论平行垂直1l与2l21//ee21ee1l与111ne11//ne1与221//nn21nn2、相关说明：上表给出了用向量研究空间线线、线面、面面位置关系的方法，判断的依据是相关的判定与性质，要理解掌握。例1证明：在平面内的一条直线，如果它和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。（三垂线定理）已知：如图,OB是平面的斜线，O为斜足，AB，A为垂足，OACDCD,求证：OBCD证明：0OACDOACDAB0ABCDABCDABOAOB0)(ABCDOACDABOACDOBCDABCD例2证明：如果一条直线和平面内的两条相交直线垂直，那么这条直线垂直于这个平面。（直线于平面垂直的判定定理）已知：Bnmnm,,，nlml,求证：l思考思考小结例题分析αlmlnlglABCA1B1C1Myz四、练习五、小结证明：在内任作一条直线g，在直线nmgl,,,上分别取向量gnml,,,nymxg所以nlymlxnymxlgl)(因为nlml,所以0,0nlml可得0gl即gl例3在直三棱柱111CBAABC中，090ACB,030BAC,MAABC,6,11是1CC得中点。求证：AMBA1证明：如图，建立空间坐标系)26,0,0(),0,0,3(),0,1,0(),6,0,3(1MABA)6,1,3(),26,0,3(1BAAM01BAAM总结：用向量证明比几何方法证明简单、明了。4、课堂练习：棱长为a的正方体ABCD—A1B1C1D1中，在棱DD1上是否存在点P使B1D⊥面PAC？解：以D为原点建立如图所示的坐标系，设存在点P（0，0，z），AP�=(-a,0,z)，AC�=(-a,a,0)，1DB�=(a,a,a)，∵B1D⊥面PAC，∴01APDB，01ACDB∴－a2+az=0新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆∴z=a，即点P与D1重合新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆∴点P与D1重合时，DB1⊥面PAC新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆本课主要研究垂直问题分析思考巩固练习ABCDA1B1C1D1Pxzy课后反思学生做题思路清晰，运用公式恰当，完成教学目标。