必修3第5章算法初步(算法案例)修改稿VIP免费

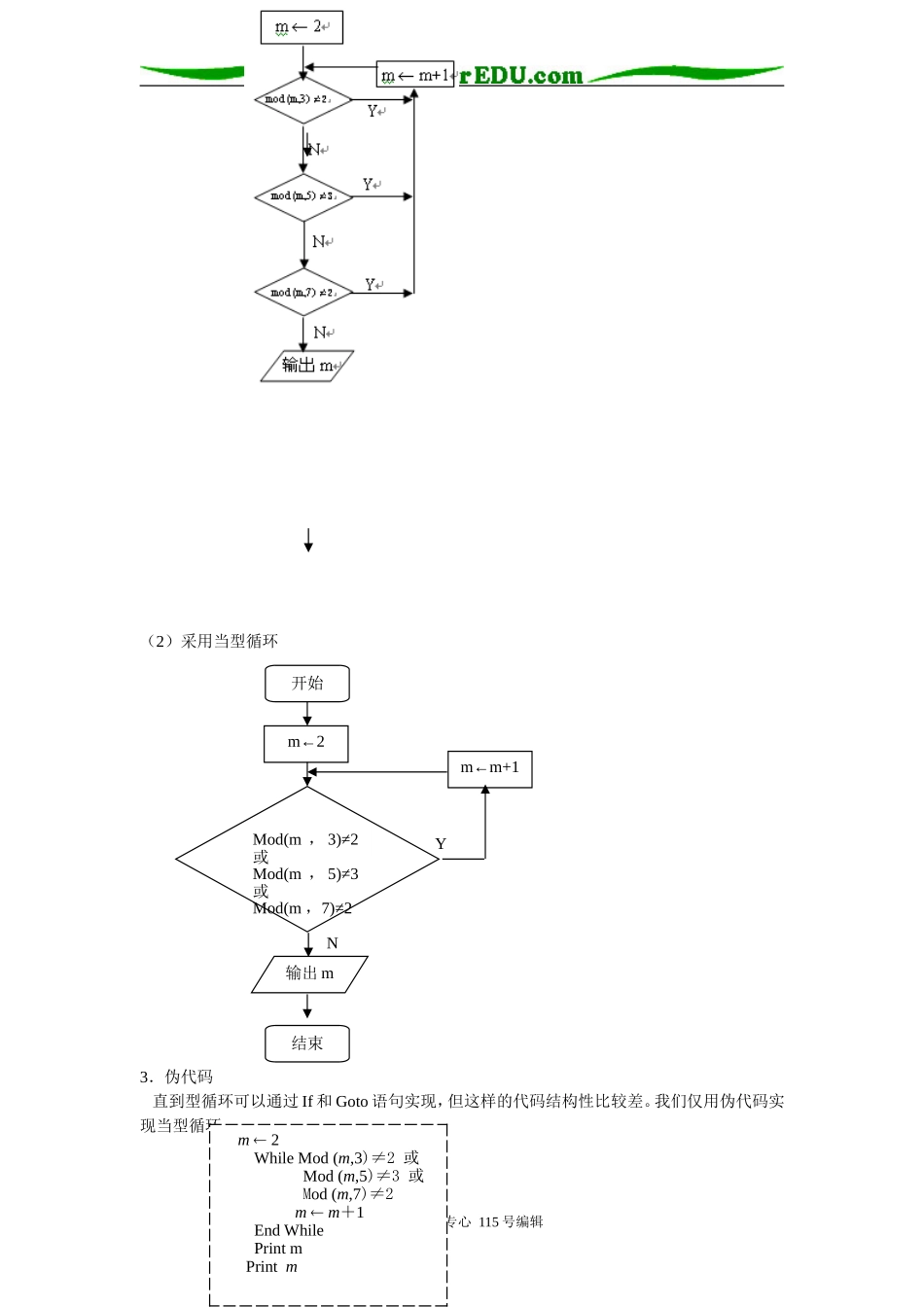
§5.44算法案例（3课时）金陵中学戴喜朱骏教学目标：1．能综合运用所学的算法知识解决实际问题，会用自然语言，流程图和伪代码表述问题的算法过程。2．综合运用算法的知识，体验我们古代悠久灿烂的数学文化。教学重点：中国剩余定理，辗转相除法，二分法中的算法思想。教学难点：用流程图和相应的伪代码表述辗转相除法，二分法。第一课时一、问题情境1．韩信点兵－孙子问题我国古代对数学作出了巨大的贡献，其中“中国剩余定理”比较著名。“中国剩余定理”是“孙子问题”的通用解法。“孙子问题”记载在《孙子算经》中，原文是：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”《孙子算经》中给出了求解关键的步骤，南宋数学家秦秋韶对该问题加以了推广，又发现了一种新的算法，叫“大衍求一术”。后来这种解法传到欧洲，欧洲学者发现此解法和高斯的解法上是一致的，但比高斯早了500余年。孙子问题的算法名称很多，宋代周密称为“鬼谷算”、“隔墙算”。宋代杨辉﹝1275﹞称为“秦王暗点兵”、“剪管术”，明代程大位叫它“物不知总”、“韩信点兵”。2．孙子问题的现代数学描述“孙子问题”相当于求关于x,y,z的方程组的正整数解。上面的方程组称为不定方程组，这类方程组中未知数的个数通常多于方程的个数。二、算法设计一些特定类型的不定方程，可以通过数论中的知识求解，但有了计算机以后，我们可以利用计算机逐个搜索的方法去寻找满足条件的解。1．自然语言（1）如何依次检索正整数？（采用循环结构）（2）该循环何时结束？（找到满足条件的整数为止）（3）一个正整数m什么时候满足方程？m同时满足被3除余2，被5除余3，被7除余2。说明：m被3除余2用符号表示为Mod(m，3)＝2；m被5除余3用符号表示为Mod(m，5)＝3；m被7除余3用符号表示为Mod(m，7)＝2；2．流程图学生活动：如何用流程图描述你的算法？可能出现以下两种描述：（1）采用直到型循环：用心爱心专心115号编辑开始结束（2）采用当型循环3．伪代码直到型循环可以通过If和Goto语句实现，但这样的代码结构性比较差。我们仅用伪代码实现当型循环。用心爱心专心115号编辑开始m←2Mod(m，3)≠2或Mod(m，5)≠3或Mod(m，7)≠2m←m+1输出m结束YNm2WhileMod(m,3)≠2或Mod(m,5)≠3或Mod(m,7)≠2mm＋1EndWhilePrintmPrintm4．利用VBA实现代码程序说明：1．“≠”VB语言中用<>表示；2．Mod(m,3)在VB中用mMod3表示；3．VB程序中“Or”表示“或”4．VB程序中使用了符号“_”表示下一行和该行是一个完整的语句。三、数学运用本节课我们利用循环结构实现了数字的搜索问题，而且学习了使用逻辑运算符“Or”实现了多种约束条件的判断。例有3个连续的自然数，其中最小的能被15整除，中间的能被17整除，最大的能被19整除，求满足要求的一组三个连续的自然数。分析：本题的其实就是求解不定方程组算法：S1取m＝1；S2当m不能被15整除，或m＋1不能被17整除，或m＋2不能被19整除，则mm＋1，转S2；否则输出m，m＋1，m＋2，算法结束；流程图：用心爱心专心115号编辑开始m←1Mod(m，15)≠0或Mod(m＋1，17)≠0或Mod(m＋2，19)≠0m←m+1输出m，m+1，m+2结束YN伪代码：思考：以下伪代码是否可行？四、回顾反思1．韩信点兵－孙子问题的求解算法；2．利用循环结构实现整数的搜索；3．利用逻辑运算符Or实现多条件的判断。五、作业P34复习题9第二课时一、问题情境用心爱心专心115号编辑m1WhileMod(m,15)≠2或Mod(m＋1,17)≠0或Mod(m＋2,19)≠0mm＋1EndWhilePrintm，m+1，m+2Printmk1a15kWhileMod(a＋1,17)≠0或Mod(a＋2,19)≠0kk＋1a15kEndWhilePrinta,a＋1,a＋2Printm在小学，我们学过求两个正整数的最大公约数的方法，先用两个数公有的质因数连续去除，一直到所得的商是互质数为止，然后把所以的除数乘起来。当两个数公有的质因数较大时（如204与85），使用上述方法求最大公约数连续去除就比较困难，下面给大家介绍一种古老而有效的方法——辗转相除法。引例1求204与85的最大公约数。204＝85×2＋34从这一步说明，204与85的最大公约数也应该是85与34的最大公约数。85＝34×2＋17从这一步说明，85与34的最大...