正弦定理和余弦定理VIP免费

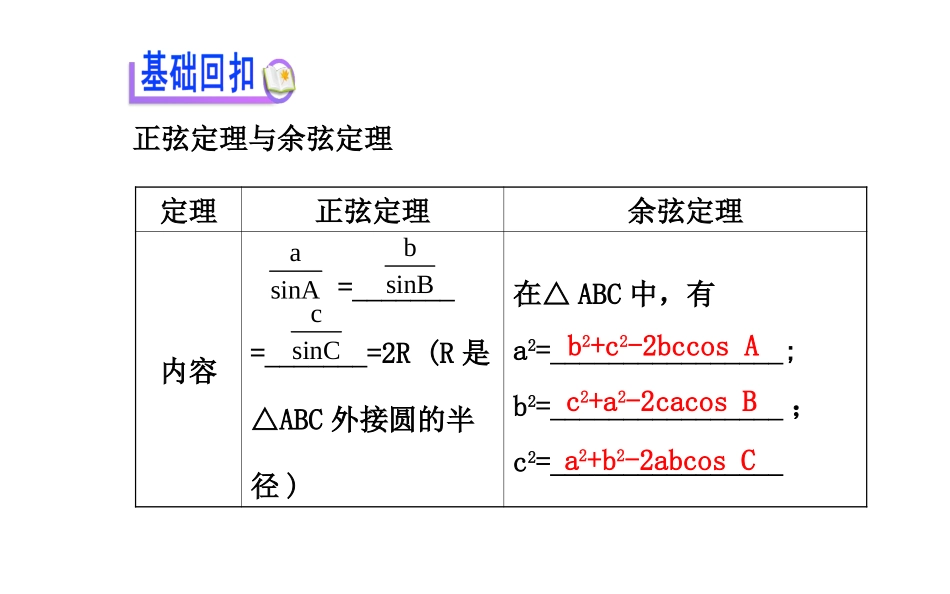
正弦定理和余弦定理临泉实验中学主讲人：孟伟正弦定理与余弦定理定理正弦定理余弦定理内容=_______=_______=2R(R是△ABC外接圆的半径)在△ABC中，有a2=________________;b2=________________；c2=________________bsinBasinAcsinCb2+c2-2bccosAc2+a2-2cacosBa2+b2-2abcosC定理正弦定理余弦定理变形公式①a=________,b=________,c=_________；②sinA∶sinB∶sinC=________；③sinA=sinB=____,sinC=____；④cosA=__________;cosB=___________;cosC=___________222bca2bc222acb2ac222abc2ab2RsinA2RsinB2RsinCa∶b∶ca,2Rb2Rc2RabcsinAsinBsinCabcsinAsinBsinC定理正弦定理余弦定理解决的问题①已知两角和任一边，求其他边和角②已知两边和其中一边的对角，求其他边和角①已知三边,求各角②已知两边和它们的夹角,求第三边和其他角判断下面结论是否正确(请在括号中打“√”或“×”).(1)在△ABC中，A＞B必有sinA＞sinB.()(2)正弦定理对钝角三角形不成立.()(3)在△ABC中共有三个角、三个边六个量，可以已知三个量求另外三个量.()(4)余弦定理对任何三角形均成立.()(5)正弦定理可以实现边角互化，但余弦定理不可以.()【解析】(1)正确. A＞B,∴a＞b,由正弦定理可得又sinB＞0,∴sinA＞sinB.(2)错误.正弦定理对任意三角形均成立.(3)错误.当已知三个角时不能求三边.a1,b＞asinA1.bsinB＞(4)正确.由余弦定理推导过程可知对任意三角形均适用.(5)错误.余弦定理可以实现角化边，也能实现边化角.答案:(1)√(2)×(3)×(4)√(5)×1.在△ABC中，a=3,A=30°,B=60°，则b等于()【解析】选A.由正弦定理得3A33B3CD23233asinB3sin602b33.1sinAsin3022.在△ABC中，a=4,C=30°，则边c等于()【解析】选B.由余弦定理得b23,A3B2C23D32223cab2abcosC161224234,c2.23.△ABC满足acosB=bcosA，则△ABC的形状为()(A)直角三角形(B)等边三角形(C)等腰三角形(D)等腰直角三角形【解析】选C.由acosB=bcosA及正弦定理得，sinAcosB=sinBcosA，即sinAcosB-cosAsinB=0,故sin(A-B)=0. A,B为△ABC的内角，∴A-B=0，∴A=B,所以△ABC是等腰三角形.4.在△ABC中，B＝30°，C＝120°，则a∶b∶c＝____.【解析】A＝180°－30°－120°＝30°，由正弦定理得，a∶b∶c＝sinA∶sinB∶sinC＝1∶1∶答案:1∶1∶3.35.在△ABC中，已知a2＝b2＋bc＋c2，则角A等于_____.【解析】由已知得b2＋c2－a2＝－bc，∴cosA＝又 0＜A＜π，答案:222bca12bc2＋－＝－，2A.3＝23考向1正弦定理的应用【典例1】(1)△ABC的内角A,B,C的对边分别是a,b,c,若B=2A,a=1,b=,则c=()(A)2(B)2(C)(D)1323(2)如图,在△ABC中，点D在BC边上，①求sin∠ABD的值;②求BD的长.53AD33,sinBAD,cosADC.135【思路点拨】(1)根据角的关系结合正弦定理求出角A,然后求出角B,C后再求解.(2)①利用∠ABD=∠ADC-∠BAD及两角差的正弦公式求解；②利用正弦定理求解.【规范解答】(1)选B.由B=2A,则sinB=sin2A，由正弦定理知即所以cosA=，所以A=，B=2A=，所以C=π－B－A=，所以c2=a2+b2=1+3=4，故c=2.ab,sinAsinB1333,sinAsinBsin2A2sinAcosA32632223(2)cosADC54sinADC1cosADC.55sinBAD1312cosBAD1sinBAD.13ABDADCBAD,①因为，所以因为，所以因为sinABDsin(ADCBAD)sinADCcosBADcosADCsinBAD4123533.51351365ABDBDAD,sinBADsinABD533ADsinBAD13BD25.33sinABD65所以②在中，由正弦定理，得所以(3)三角形中等边对等角,大边对大角,反之亦然;三角形中任意两边之和大于第三边,任意两边之差小于第三边.【变式训练】1.已知△ABC中，a,b,c分别是角A,B,C的对边，，B=60°，则A=()(A)135°(B)45°(C)135°或45°(D)90°【解析】选B.依题意，由正弦定理得，解得sinA=，又b＞a，∴A=45°.a2b3，absinAs...