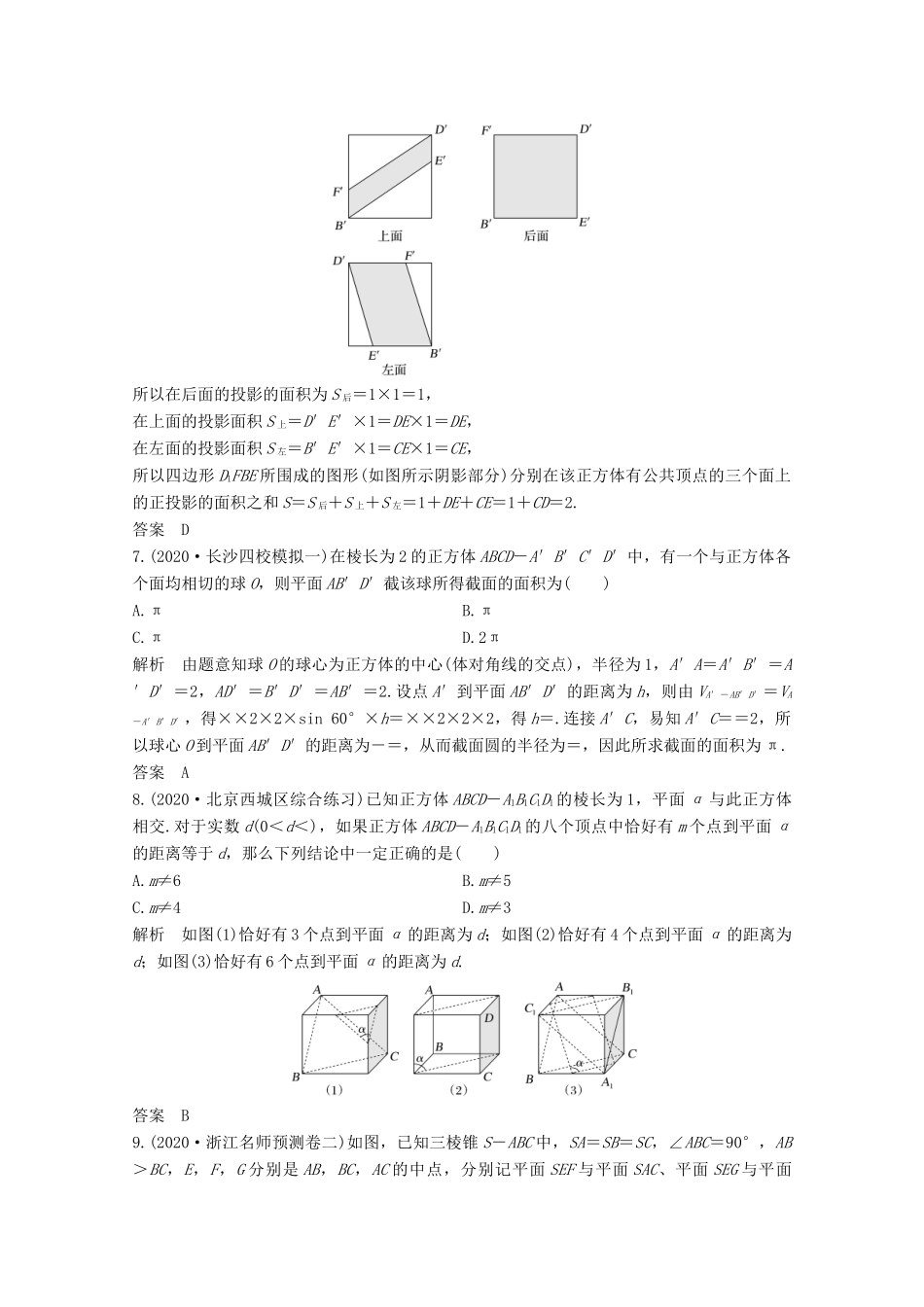
加强练(八)立体几何与空间向量一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2015·上海卷)如图,四个棱长为1的正方体排成一个正四棱柱,AB是一条侧棱,Pi(i=1,2,…,8)是上底面上其余八个点,则AB·APi(i=1,2,…,8)的不同值的个数为()A.1B.2C.4D.8解析 AB·APi=|AB|·|APi|cos〈AB,APi〉=1×1=1,∴只有一个值.答案A2.(2020·宁波模拟)若直线l不平行于平面α,且l⊄α,则()A.α内所有直线与l异面B.α内只存在有限条直线与l共面C.α内存在唯一的直线与l平行D.α内存在无数条直线与l相交解析由直线与平面的位置关系知l⊄α,则l∥α或l与平面α相交.由题意知,l不平行于平面α,则设l∩α=P,故平面α内所有过点P的直线与l相交,平面α内不过点P的直线与l异面,故选D.答案D3.如图,斜线段AB与平面α所成的角为60°,B为斜足,平面α上的动点P满足∠PAB=30°,则点P的轨迹是()A.直线B.抛物线C.椭圆D.双曲线的一支解析利用平面截圆锥面直接得轨迹.因为∠PAB=30°,所以点P的轨迹为以AB为轴线,PA为母线的圆锥面与平面α的交线,且平面α与圆锥的轴线斜交,故点P的轨迹为椭圆.答案C4.(2017·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.+1B.+3C.+1D.+3解析由几何体的三视图可知,该几何体是一个底面半径为1,高为3的圆锥的一半与一个底面为直角边长是的等腰直角三角形,高为3的三棱锥的组合体,所以该几何体的体积V=×π×12×3+××××3=+1.答案A5.已知正方体ABCD-A1B1C1D1的棱长为,正方体所在空间的动点P满足|PB1+PC|=2,则AP·AD1的取值范围是()A.[0,4]B.[1,4]C.[0,2]D.[1,2]解析因为正方体的棱长为,所以B1C=2,则由|PB1+PC|=2得点P在以B1C的中点为球心,为半径的球面上.当点P与点B重合时,点P在直线AD1上的射影为点A,当点P与点C1重合时,点P在直线AD1上的射影为点D1,则AP·AD1∈[0,|AD1|2]=[0,4],故选A.答案A6.(2020·北京朝阳区模拟)在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为线段CD和A1B1上的动点,且满足CE=A1F,则四边形D1FBE所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和()A.有最小值B.有最大值C.为定值3D.为定值2解析依题意,设四边形D1FBE的四个顶点在后面,上面,左面的投影点分别为D′,F′,B′,E′,则四边形D1FBE在上面,后面,左面的投影分别如下图.所以在后面的投影的面积为S后=1×1=1,在上面的投影面积S上=D′E′×1=DE×1=DE,在左面的投影面积S左=B′E′×1=CE×1=CE,所以四边形D1FBE所围成的图形(如图所示阴影部分)分别在该正方体有公共顶点的三个面上的正投影的面积之和S=S后+S上+S左=1+DE+CE=1+CD=2.答案D7.(2020·长沙四校模拟一)在棱长为2的正方体ABCD-A′B′C′D′中,有一个与正方体各个面均相切的球O,则平面AB′D′截该球所得截面的面积为()A.πB.πC.πD.2π解析由题意知球O的球心为正方体的中心(体对角线的交点),半径为1,A′A=A′B′=A′D′=2,AD′=B′D′=AB′=2.设点A′到平面AB′D′的距离为h,则由VA′-AB′D′=VA-A′B′D′,得××2×2×sin60°×h=××2×2×2,得h=.连接A′C,易知A′C==2,所以球心O到平面AB′D′的距离为-=,从而截面圆的半径为=,因此所求截面的面积为π.答案A8.(2020·北京西城区综合练习)已知正方体ABCD-A1B1C1D1的棱长为1,平面α与此正方体相交.对于实数d(0<d<),如果正方体ABCD-A1B1C1D1的八个顶点中恰好有m个点到平面α的距离等于d,那么下列结论中一定正确的是()A.m≠6B.m≠5C.m≠4D.m≠3解析如图(1)恰好有3个点到平面α的距离为d;如图(2)恰好有4个点到平面α的距离为d;如图(3)恰好有6个点到平面α的距离为d.答案B9.(2020·浙江名师预测卷二)如图,已知三棱锥S-ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,AC的中点,分别记平面SEF与平面SAC、平面SEG与平面SBC、平面SFG与平面SAB所成的锐二面角为α,β,γ,则α,β,γ的大小关系是()A.α<β<γB....