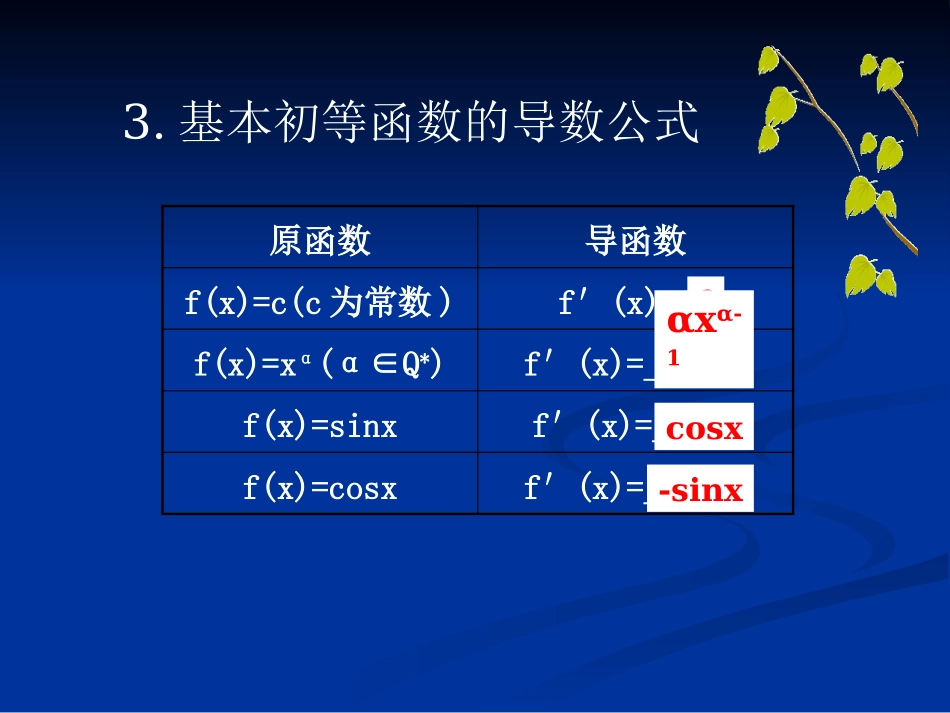
用导数求曲线的切线乐山一中谢采维1.导数的几何意义函数在点处的导数的几何意义是在曲线上点处的___________.相应地,切线方程为_____________________.切线的斜率𝒚−𝒇(𝒙𝟎)=𝒇′(𝒙𝟎)(𝒙−𝒙𝟎)2.求切线方程需要:斜率、切线上一点(点斜式)导数用导数求曲线的切线3.基本初等函数的导数公式原函数导函数f(x)=c(c为常数)f′(x)=__f(x)=xα(α∈Q*)f′(x)=______f(x)=sinxf′(x)=_____f(x)=cosxf′(x)=______0αxα-1cosx-sinx原函数导函数f(x)=ax(a>0,且a≠1)f′(x)=_____f(x)=exf′(x)=__f(x)=logax(a>0,且a≠1)f′(x)=______f(x)=lnxf′(x)=_____axlnaex1xlna1x4.导数的四则运算法则(1)[f(x)±g(x)]′=_______________.(2)[f(x)·g(x)]′=__________________(3)[]=________________(g(x)≠0).f′(x)±g′(x)f′(x)g(x)+f(x)g′(x)2fxgxfxgxgx[]例1:函数g(x)的图象如图所示,已知g(x)在P点处的切线方程为y=kx-2,则g(2)+g(2)=____________解:由题P(2,1)在切线上,代入切线方程得k=所以g(2)=k=g(2)=1g(2)+g(2)=注:(1)切线斜率k=g()(2)切点在切线上(3)切点在曲线上𝟓𝟐例2:已知函数f(x)=-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4,求a,b的值例2:已知函数f(x)=-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4,求a,b的值解:f(x)=因为曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4所以所以a=b=4例3.已知曲线上的一点P(2,),求过点P的切线方程解:y==4所以切线:y=4(x-2)+即:4x-y-8+=012x-3y-16=0思考思考:怎样修改题目才能使刚才的解法正确呢?已知曲线上的一点P(2,),求在点P处的切线方程如果不改题,这道题应该怎么解?此时,P为切点在例3:已知曲线上的一点P(2,),求过点P的切线方程解:设切点(,)k=y切线方程:y-=(x-)切线过点P(2,)且(,)在曲线上由(1)(2)得-3+4=0即(+1)=0即=2或=-1当=2时,=,切线:12x-3y-16=0当=-1时,=-切线:3x-3y+2=0例3已知曲线上的一点P(2,),求过点P的切线方程练习1:函数g(x)的图象如图所示,已知g(x)在P点处的切线方程为y=kx-1,则g(1)+g(1)=____________3练习2:求曲线解:设切点(,)k=y切线方程:y-=(x-)切线过点P(2,)且(,)在曲线上由(1)(2)得-3+4=0即(+1)=0即=2或=-1故所求的切线方程为4x-y-4=0或x-y+2=0练习2:求曲线y=+1.公式:2.切点(1)切线斜率k=g()(2)切点在切线上(3)切点在曲线上3.区别总结谢谢练习3:已知函数+,若曲线与曲线在它们的交点处具有公共切线,求的值。练习3:已知函数f(x)=a+,若曲线f(x)与曲线g(x)在它们的交点(1,C)处具有公共切线,求的值。解:因为为公共切点,所以所以(1)又因为所以又因为曲线与曲线在它们的交点处具有公共切线所以(2)由(1)(2)得