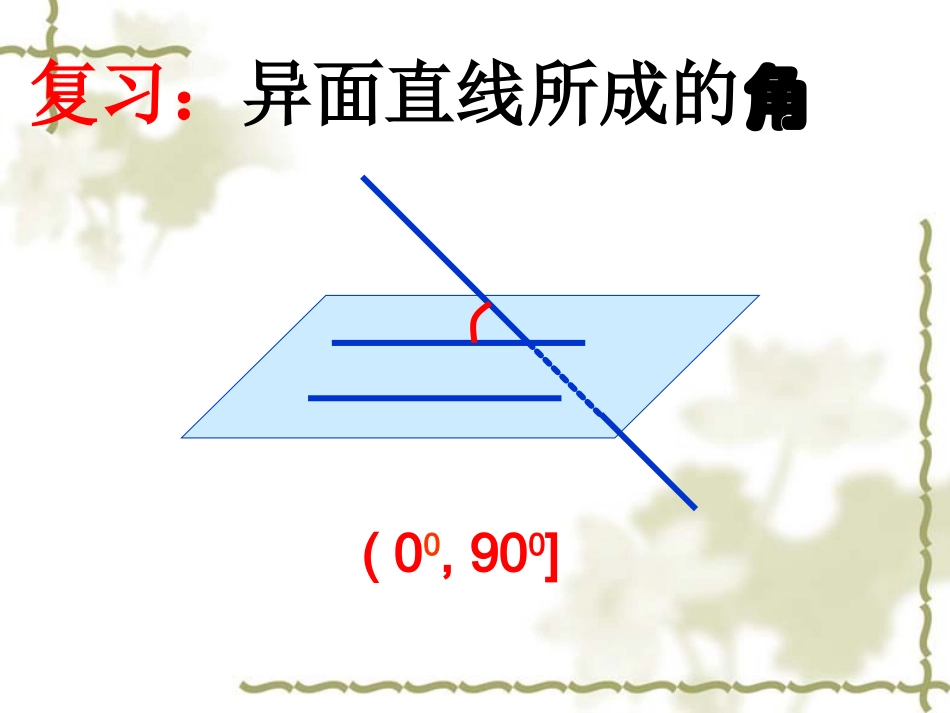
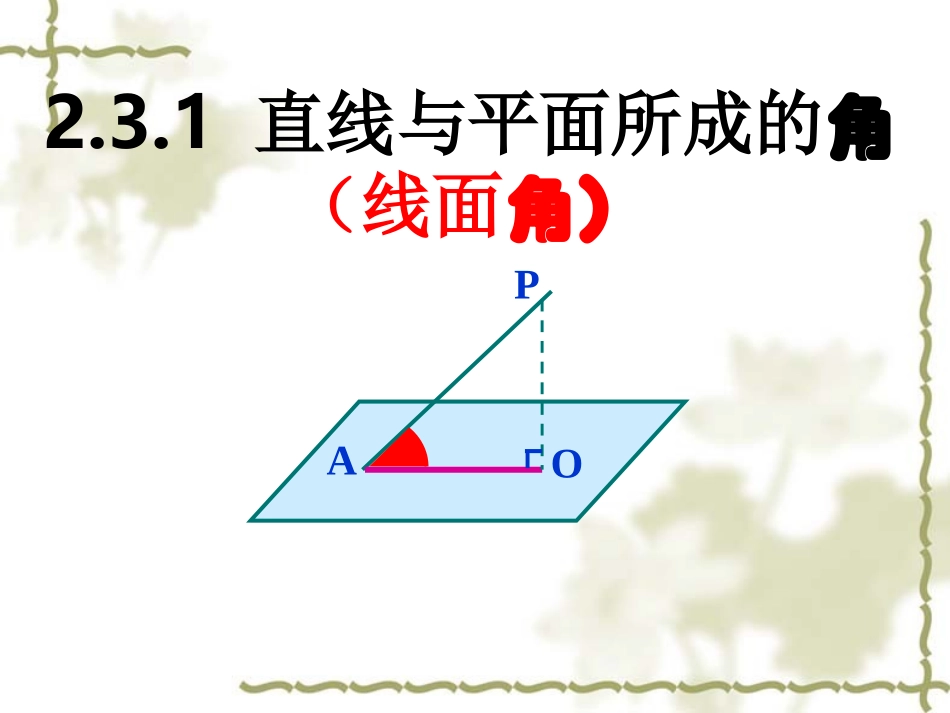
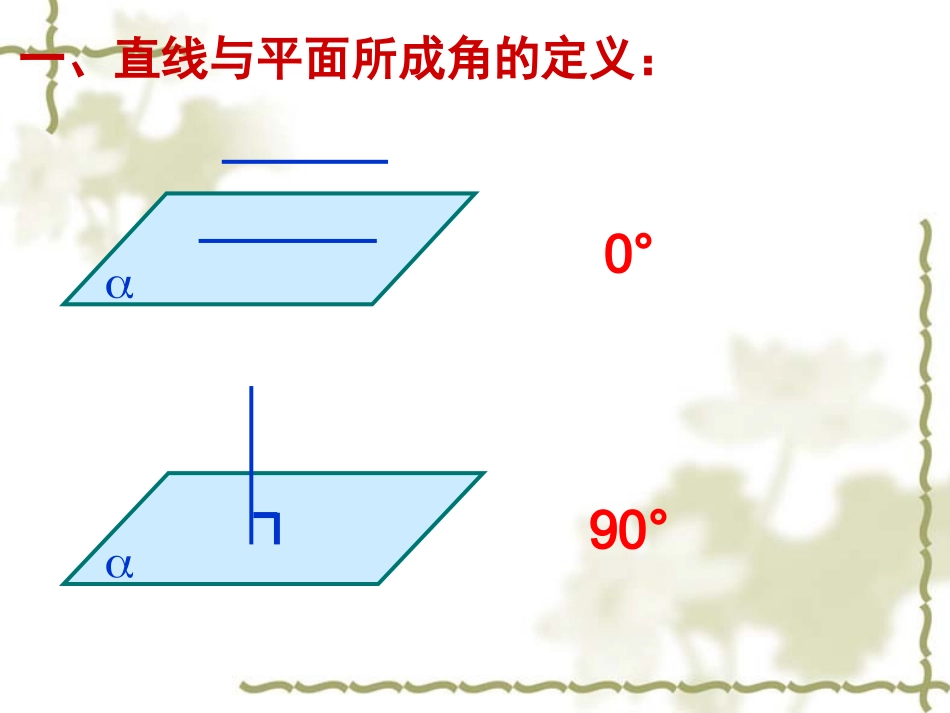
复习:异面直线所成的角(00,900]2.3.1直线与平面所成的角(线面角)PAO一、直线与平面所成角的定义:0°90°斜线和平面所成角:斜线和它在平面内的射影所成的锐角。(00,900)PAO斜线垂线斜足垂足斜线在平面上的射影直线与平面所成的角的范围:[00,900]PAO(00,900)90000异面直线所成的角的范围:(00,900](1)先判断直线与平面的位置关系(2)当直线与平面斜交时,常采用以下步骤:①作出或找出斜线上的点到平面的垂线②作出或找出斜线在平面上的射影③证明所作角即为线面角④解由斜线段,射影,垂线段构成的直角三角形,求出线面角二、线面角的求法PAO例1、如图:正方体ABCD-A1B1C1D1中,求:(1)A1C1与面ABCD所成的角A1D1C1B1ADCB0o1、如图:正方体ABCD-A1B1C1D1中,求:(2)A1C1与面BB1D1D所成的角A1D1C1B1ADCB90o1、如图:正方体ABCD-A1B1C1D1中,求:(3)A1C1与面BB1C1C所成的角A1D1C1B1ADCB45o1、如图:正方体ABCD-A1B1C1D1中,求:(4)A1C1与面ABC1D1所成的角A1D1C1B1ADCBE30oA1B1C1D1ABCD练习、如图,正方体ABCD-A1B1C1D1中,求(1)直线A1B和平面BCC1B1所成的角。45oA1B1C1D1ABCD练习、如图,正方体ABCD-A1B1C1D1中,求(2)直线A1B和平面A1B1CD所成的角。O30o例2、如图,在正方体ABCD-A1B1C1D1中,O为下底面AC的中心,求A1O与平面BB1D1D所成的角的正弦值。ABCDA1B1C1D1OO133例3、正四面体P—ABC中,求侧棱PA与底面ABC所成的角余弦值。PABCHD33归纳小结3.数学思想方法:转化的思想空间问题平面问题2.线面角的求法1.线面角的概念及范围090范围:,PAOAPOa补充:三垂线定理a,PO,PA的斜线是平面AOaPAaPAaAOa则若则若,2,1判断下列说法是否正确(1)两条平行直线在同一平面内的射影一定是平行直线()(2)两条相交直线在同一平面内的射影一定是相交直线()(3)两条异面直线在同一平面内的射影要么是平行直线,要么是相交直线()(4)若斜线段长相等,则它们在平面内的射影长也相等()