3.3.1单调性VIP免费

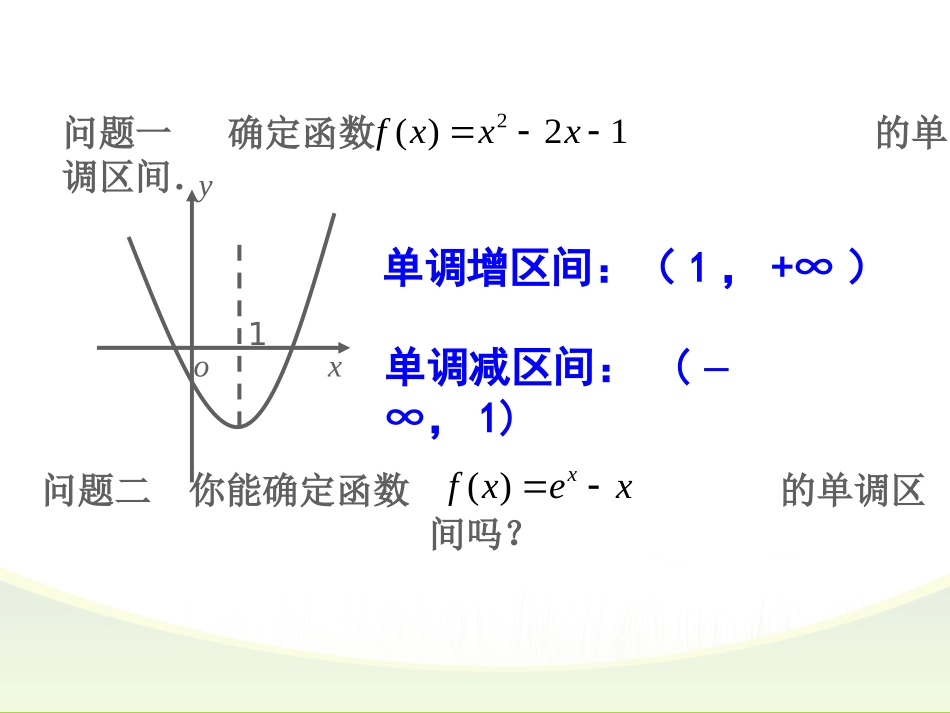
导数在研究函数中的应用——单调性问题一确定函数的单调区间．2()21fxxxyox1单调增区间：（1，+∞）单调减区间：(－∞，1)问题二你能确定函数的单调区间吗？()xfxex问题三能不能利用导数研究函数的单调性呢？函数单调增图像逐渐上升切线的斜率大于零12,xxI任意()0fx1212()()0fxfxxx1212()()xxfxfx当时有aby=f(x)xoyy=f(x)xoyab导数与函数单调性的联系：如果在某区间上，那么为该区间上的增函数，()0fx()fx一般地，对于函数()yfx如果在某区间上，那么为该区间上的减函数．()0fx()fx例1求下列函数的单调区间：（1）（2）()lnfxxx()xfxex问题四利用导数求函数单调区间的步骤是：32().fx．根据的结果确定函数的单调区间2()()0()0;fxfxfx．在函数的内解不等式和定义域1、确定定义域，并求导函数；xf'例2求证：函数在区间上是单调减函数．xxxfln10，问题五你能利用导数作出函数的草图吗？3()fxxx例3已知方程有三个不同的实数解，则实数m的取值范围为．30xxm试结合思考：如果函数在某区间上单调递增，那么在该区间上是否必有导数大于零？3()fxx思考：已知函数在定义域上单调增，求实数m的取值范围．2ln2fxmxxx课堂练习：1、求函数的单调递减区间；2、求函数在上的单调增区间；3、若函数在区间上单调递增，求的取值范围。21ln2yxxsinxyex0,()lnfxkxx1,k4、已知函数，当时，讨论的单调性。12ln2fxaxaxx0axf课堂小结：1．通过本节课的学习，你学到了哪些新知识？能解决哪些问题？2．本节课我们用到了哪些数学思想方法？