1.3.1单调性VIP免费

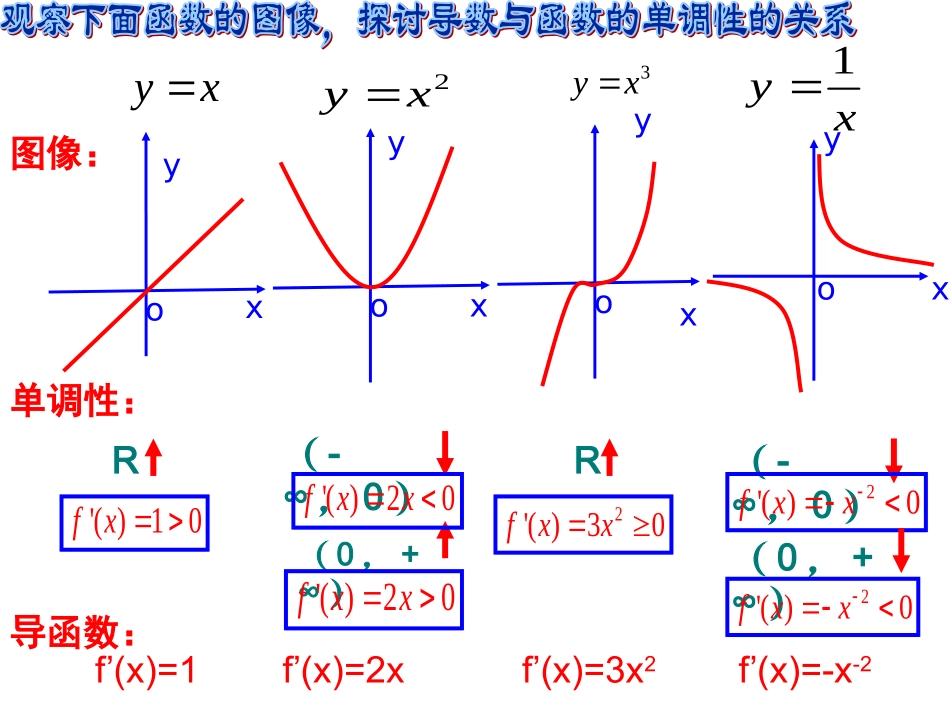
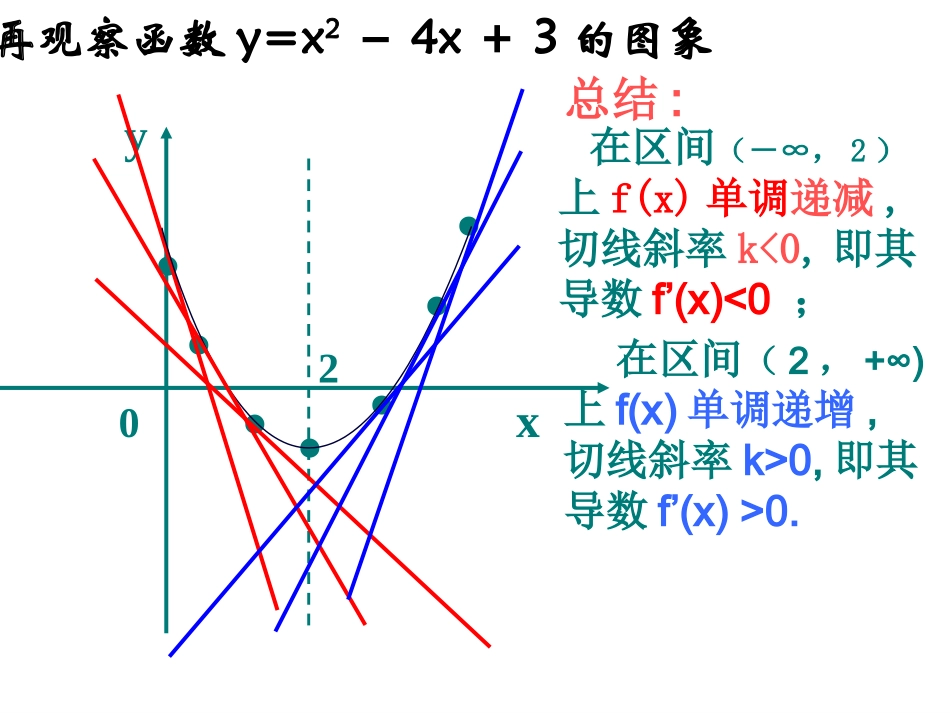
yoxxyoxyoxy1yx2yx3yxR'()10fx（-∞，0）（0，+∞）'()20fxx'()20fxxR2'()30fxx（-∞，0）2'()0fxx（0，+∞）2'()0fxxyox单调性：图像：导函数：f’(x)=1f’(x)=2xf’(x)=3x2f’(x)=-x-22yx0.......再观察函数y=x2－4x＋3的图象在区间（－∞，2）上f(x)单调递减,切线斜率k<0,即其导数f’(x)<0；总结:在区间（2，+∞)上f(x)单调递增,切线斜率k>0,即其导数f’(x)>0.如果在某个区间内恒有f’(x)＝0，那么函数f(x)有什么特性？ab(,)在某个区间内,fx'()0fxab()(,)在内单调递增fx'()0fxab()(,)在内单调递减在此区间内恒有f(x)＝c（c为常数），无单调性应用判断函数32()23121fxxxx的单调性，并求出其单调区间.判断函数32()23121fxxxx的单调性，并求出其单调区间.因为32()23121fxxxx所以2'()6612fxxx12即或时，xx当21即时，x函数单调递减。'()0,fx'()0，fx函数的单调递增区间为单调递减区间为（-2，1）(1)(,2)，和应用函数单调递增；当=6（x+2）(x-1)f(x)f(x)f(x)函数单调递增；=6（x+2）(x-1)f(x)f(x)判断函数32()23121fxxxx的单调性，并求出其单调区间.你能小结求解函数单调区间的步骤吗？你能小结求解函数单调区间的步骤吗？（1）确定函数y=f(x)的定义域；（2）求导数f’(x)；（3）解不等式f’(x)>0，解集在定义域内的部分为增区间；（4）解不等式f’(x)<0，解集在定义域内的部分为减区间．应用设是函数的导函数，的图象如右图所示,则的图象最有可能的是()()fx'()fx'()yfx()yfxxyo12()yfxxyo12()yfx(A)(B)xyo12()yfxxyo12()yfx(C)(D)xyo'()yfx2高考链接C导学案习题选做题：课本31页习题1.3A组1，2必做题：