高二数学 双曲线的简单几何性质选修2VIP免费

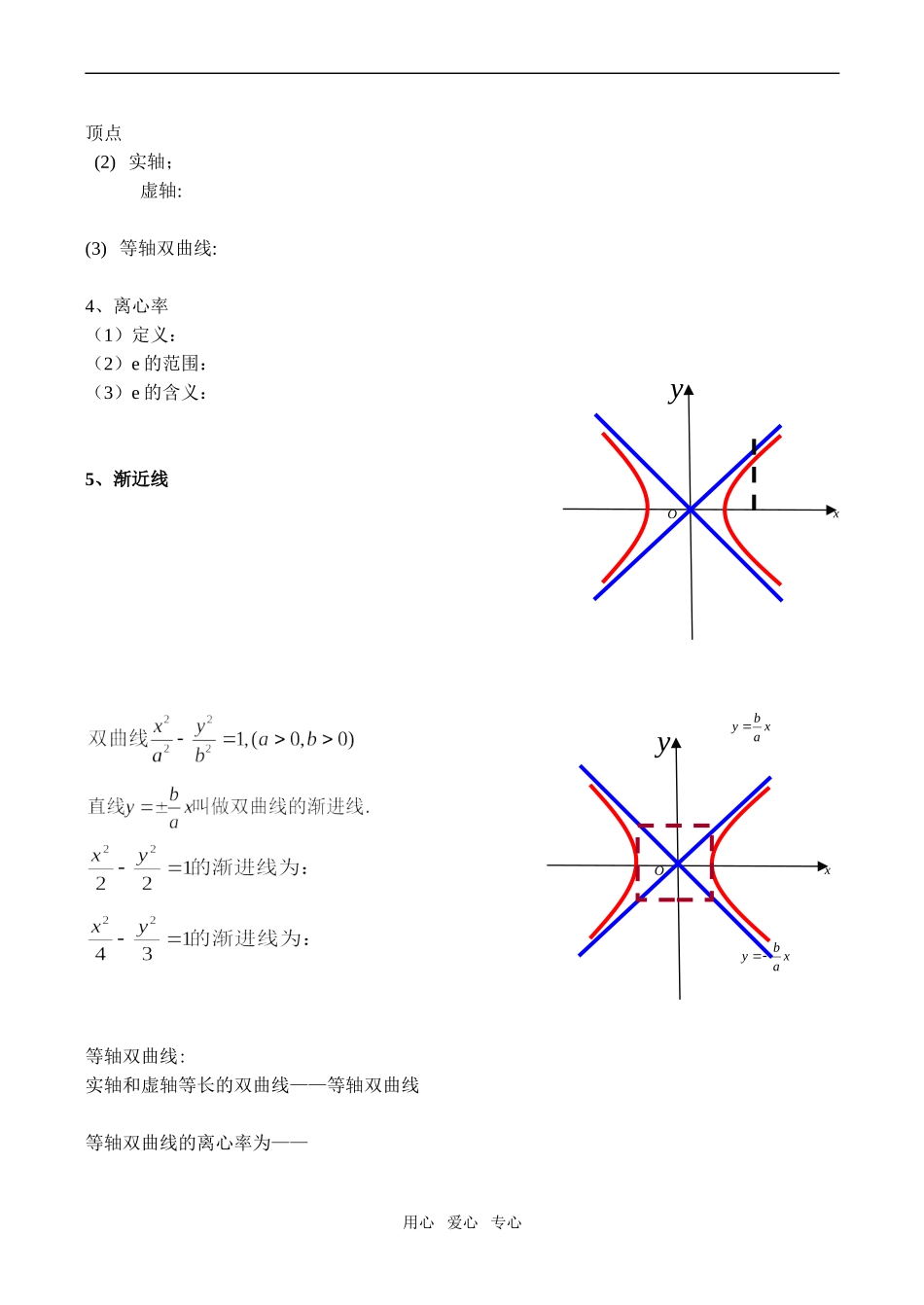
高二数学选修2双曲线的简单几何性质一、教学目标1．了解双曲线的简单几何性质，如范围、对称性、顶点、渐近线和离心率等。2．能用双曲线的简单几何性质解决一些简单问题。二、教学重点、难点重点：双曲线的几何性质及初步运用。难点：双曲线的渐近线。三、教学过程(一)复习提问引入新课一、复习回顾：1.双曲线的标准方程:形式一：形式一：2.椭圆的图像与性质:类比椭圆的几何性质，我们来共同探究双曲线的几何性质。二、讲授新课：一、研究双曲线的简单几何性质1、范围2、对称性3、顶点（1）双曲线与对称轴的交点，叫做双曲线的用心爱心专心标准方程范围对称性顶点焦点对称轴离心率A1顶点(2)实轴；虚轴:(3)等轴双曲线:4、离心率（1）定义：（2）e的范围：（3）e的含义：5、渐近线等轴双曲线:实轴和虚轴等长的双曲线——等轴双曲线等轴双曲线的离心率为——用心爱心专心xyOxyOxabyxaby等轴双曲线的两渐近线为y=±x,互相垂直(所成角为90°).(2000高考)双曲线的两条渐近线互相垂直,那么该双曲线的离率是小试牛刀:(5）渐近线方程：用心爱心专心图形方程范围对称性顶点离心率渐进线xyO2A1A1F2F（五）例题讲解例1.求双曲线9x2-16y2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。例2.求证(1)双曲线的焦点到渐近线的距离等于虚半轴的长b.练习.已知双曲线的对称轴为坐标轴,两个顶点间的距离为2,焦点到渐近线的距离为,求双曲线的方程双曲线中的第二个特征三角形(2)过双曲线的焦点与实轴垂直的直线被双曲线截得的弦长为双曲线中通径长公式例3.(1)若双曲线的两个端点把两焦点间的距离三等分,则双曲线的离心率为.(2)若双曲线的渐近线方程为则双曲线的离为.(3).双曲线与的离心率分别为和,则的最小值为.用心爱心专心例4(1).已知双曲线的焦点在y轴上,焦距为16,离心率是4/3,求双曲线的标准方程.(2)已知双曲线的渐近线是x±2y=0,并且双曲线过点,求双曲线方1、共渐近线双曲线的方程的设法:以bx±ay=0为渐近线的双曲线可设为=λ(λ≠0)2、小结:1.双曲线的简单几何性质，如范围、对称性、顶点、渐近线和离心率等2.双曲线的几何性质的初步运用。作业：课本P41：练习1，2，3，4用心爱心专心