垂径定理~~杨婷VIP免费

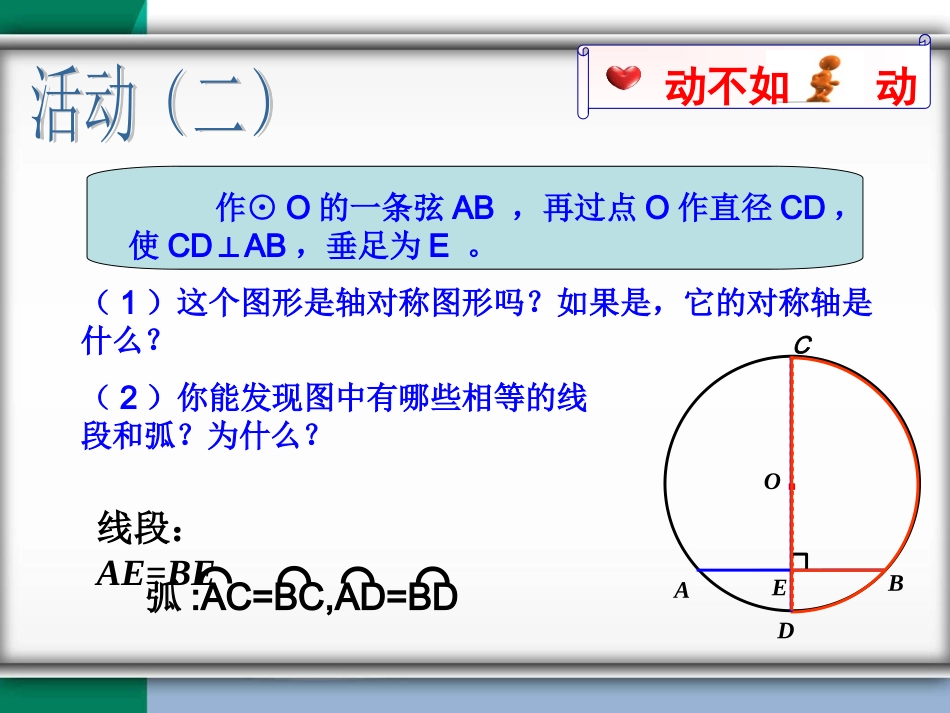
谢坊初中：杨婷将你手中的圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？可以发现：1、圆是轴对称图形。2、任何一条直径所在直线都是它的对称轴。不借助任何工具，你能找到一张圆形纸片的圆心吗?动不如动·OABDEC作⊙O的一条弦AB，再过点O作直径CD，使CDAB⊥，垂足为E。（2）你能发现图中有哪些相等的线段和弧？为什么？（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？弧:AC=BC,AD=BD⌒⌒⌒⌒线段：AE=BE动不如动·OABCDE条件CD为直径CD⊥AB垂径定理的几何语言叙述:CD为直径，AE=BE，AC=BC，⌒⌒AD=BD．⌒⌒∴结论AE=BEAC=BC⌒⌒AD=BD⌒⌒ CDAB⊥垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．定理中的径可以是直径、半径、弦心距等过圆心的直线或线段判断下列图形，能否使用垂径定理？EDCOABDCOABEEOCDABECOABEDOABEOAB动不如动动不如动·OABDEC作⊙O的一条弦AB，取AB的中点E，连接O、E并延长，交圆于C、D。（2）你能发现图中有哪些相等的弧？AB与CD有怎样的位置关系？为什么？（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？弧:AC=BC,AD=BD⌒⌒⌒⌒CDAB⊥·如果AB经过圆心，以上结论是否任然成立？·OABCDE条件CD为直径AE=BE垂径定理推论的几何语言叙述:CD为直径，CDAB⊥，AC=BC，⌒⌒AD=BD．⌒⌒∴结论CDAB⊥AC=BC⌒⌒AD=BD⌒⌒ AE=BE垂径定理的推论：平分弦的直径垂直于弦，并且平分弦所对的两条弧．（不是直径）·“知二推三”根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备：（1）过圆心（2）垂直于弦（3）平分弦（4）平分弦所对的优弧（5）平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论。注意这个弦不能是直径哦！OABE如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．例题讲解解：OEAB222AOOEAE2222=3+4=5cmAOOEAE∴⊙O的半径为5cm.118422AEAB在RtAOE△中连接OA,在⊙O中3弦心距半弦半径半径²=弦心距²+半弦²问题：你知道赵州桥吗?它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？动不如动37.4m7.2mOCDBAAB=37.4CD=7.2AO=?动不如动学以致用解：如图，设半径为R，ABAD21,7.184.3721DCOCOD.2.7R在Ｒt△AOD中，由勾股定理，得,222ODADOA.)2.7(7.18222RR即解得R≈27.9（m）.答：赵州桥的主桥拱半径约为27.9m.37.47.2AB=37.4,CD=7.2R18.7R-7.2OABCD解：如图，设半径为R CDABAB=80⊥∴AD=BD=AB=X80=40 CD=20OD=OC-CD∴OD=R–20在RtOAD△中解得R=50（m）1212222AOODAD22240(20).RR即12解：如图，设半径为R CDABAB=80⊥∴AD=BD=AB=X80=40 CD=20OD=OC-CD∴OD=R–20在RtOAD△中解得R=50（m）1212如图，有一拱形公路桥，圆弧形桥拱的水面跨度AB=80m，桥拱到水面的最大高度CD=20m，求桥拱所在圆的半径。动不如动学以致用O如图，图中的圆为同心圆变式1：AC与BD有什么关系？变式2：AC＝BD依然成立吗动不如动E解： OEAB⊥∴AE=BE,CE=DE∴AE-CE=BE-DE即AC=BDEDCOABNMDCOABDCOABDCOAB变式3：隐去（变式1）中的大圆，得右图连接OA，OB，若OA=OB，AC、BD有什么关系？为什么？变式4：隐去（变式1）中的小圆，得右图连接OC，OD，若OC=OD，AC、BD有什么关系？为什么？动不如动学以致用如图，图中的圆为同心圆EE（2）OBADC动不如动已知：AB和CD是⊙O内的两条平行弦，AB=6cm，CD=8cm，⊙O的半径为5cm，（1）请根据题意画出符合条件的图形（2）求出AB与CD间的距离。EFEFOBADC（1）1、圆是一个什么图形？圆是轴对称图形。2、你是怎么理解垂经定理及其推论的呢？垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．注意：定理中的径可以是直径、半径、弦心距等过圆心的直线或线段。通过这节课的学习，你有哪些收获？能与大家一起分享吗？通过这节课的学习，你有哪些收获？能与大家一起分享吗？解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于...