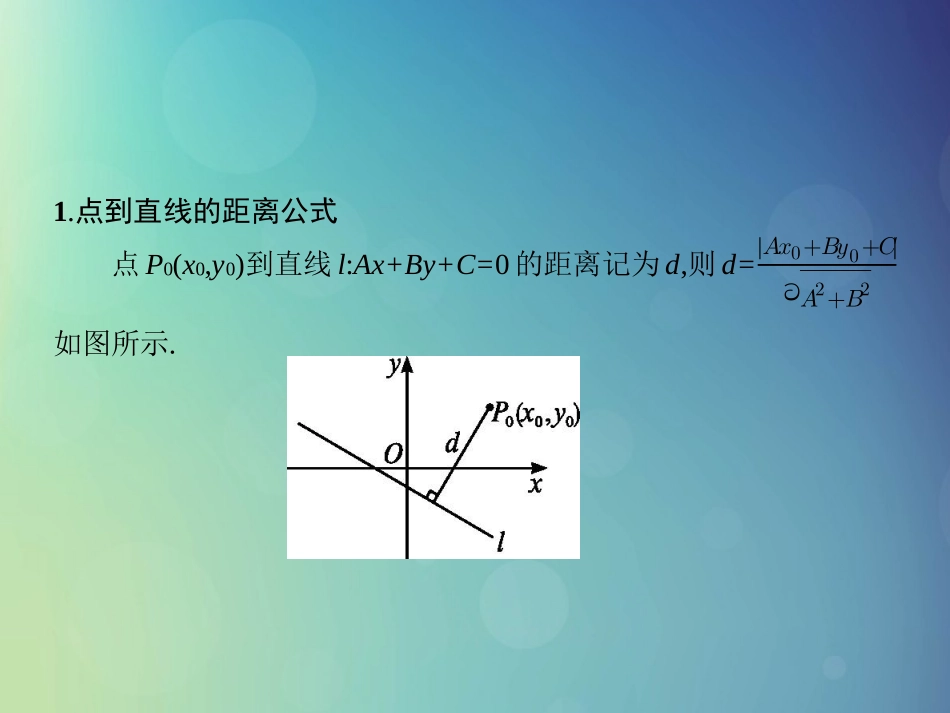
第2课时点到直线的距离公式1.掌握点到直线的距离公式.2.求点到直线的距离、两平行直线间的距离.1.点到直线的距离公式点P0(x0,y0)到直线l:Ax+By+C=0的距离记为d,则d=|𝐴𝑥0+𝐵𝑦0+𝐶|ට𝐴2+𝐵2,如图所示.名师点拨1.点到直线的距离公式的形式是:分母是直线方程Ax+By+C=0的x项、y项系数平方和的算术平方根,分子是用x0,y0替换直线方程中x,y所得实数的绝对值.2.当点P(x0,y0)在直线l上时,有Ax0+By0+C=0,即d=0.3.点到几种特殊直线的距离:①点P(x0,y0)到x轴的距离d=|y0|;②点P(x0,y0)到y轴的距离d=|x0|;③点P(x0,y0)到直线y=a的距离d=|y0-a|;④点P(x0,y0)到直线x=b的距离d=|x0-b|.【做一做1-1】点(3,1)到直线x=5的距离为()A.2B.3C.4D.8答案:A【做一做1-2】点A(-2,1)到直线y=2x-5的距离是()答案:DA.2B.10ξ33C.8ξ55D.2ξ52.两条平行直线间的距离(1)定义:夹在两条平行直线间公垂线段的长叫作这两条平行直线间的距离.(2)求法:两条平行直线l1:Ax+By+C1=0,l2:Ax+By+C2=0间的距离公式为d=|𝐶1-𝐶2|ට𝐴2+𝐵2.特别地,若两条平行直线的方程为l1:y=kx+b1,l2:y=kx+b2,则这两条平行直线间的距离d=|𝑏1-𝑏2|ට1+𝑘2.名师点拨1.公式d=|𝐶1-𝐶2|ට𝐴2+𝐵2适用于两条直线的方程都是一般式,并且两方程中x,y的系数对应相同的情况,如果两条平行直线的方程中x,y的系数不对应相同,那么必须先化为x,y的系数对应相同再应用公式.2.平行直线间的距离可以转化为点线距,即在其中一条直线上任取一点P,点P到另一条直线的距离即为平行直线间的距离,且距离与该点的位置无关.因此,在计算平行直线间距离时,可以选特殊点,比如某条直线与坐标轴的交点.解:方法一:在直线l1上取一点A(1,1),则点A到直线l2的距离即为所求的平行直线间的距离.由点到直线的距离公式,得d=|3×1+4×1-10|ට32+42=35.方法二:直线l1的方程可化为l1:3x+4y-7=0,又直线l2的方程为l2:3x+4y-10=0,由两条平行直线间的距离公式,得d=|-7-(-10)|ට32+42=35.【做一做2】求两条平行直线l1:3x+4y=7和l2:3x+4y-10=0间的距离.题型一题型二题型三题型一求点到直线的距离【例1】求点P(1,2)到下列各直线的距离:(1)l1:y=x-3;(2)l2:y=-1.分析:先将直线方程化成一般式,再利用点到直线的距离公式求解,特殊直线可采用数形结合法.题型一题型二题型三解:(1)将直线方程化为一般式为x-y-3=0,由点到直线的距离公式得d1=|1-2-3|ට12+(-1)2=2ξ2.(2)方法一:将直线方程化为一般式为y+1=0,由点到直线的距离公式得d2=|2+1|ට02+12=3.方法二: y=-1平行于x轴,如图所示,∴d2=|2-(-1)|=3.题型一题型二题型三反思求点到直线的距离,要注意应用公式的条件,其计算步骤如下:(1)直线方程不是一般式,应先化为一般式;(2)把点P的坐标直接代入公式d=|𝐴𝑥0+𝐵𝑦0+𝐶|ට𝐴2+𝐵2;(3)求出d的值.题型一题型二题型三【变式训练1】求点P(3,-2)到下列直线的距离:(1)3x-4y-1=0;(2)y=6;(3)y轴.解:(1)由点到直线的距离公式,得(2)因为直线y=6与x轴平行,所以d=|6-(-2)|=8.(3)d=|3|=3.d=|3×3-4×(-2)-1|ට32+(-4)2=165.题型一题型二题型三题型二两条平行直线间的距离【例2】求两条平行直线l1:6x+8y=20和l2:3x+4y-15=0之间的距离.分析由题目可获取以下主要信息:①l1与l2是两条定直线;②l1∥l2.解答本题可先在直线l1上任取一点A,再求点A到直线l2的距离即为两条直线间的距离;或者直接应用两条平行直线间的距离公式d=|𝐶1-𝐶2|ට𝐴2+𝐵2.解:方法一:在直线l1上取一点A(2,1),则点A到直线l2的距离即为所求的平行直线间的距离,所以l1与l2间的距离d=|3×2+4×1-15|ට32+42=1.方法二:把l1,l2的方程分别化l1:3x+4y-10=0,l2:3x+4y-15=0,则l1与l2间的距离d=|-10-(-15)|ට32+42=1.题型一题型二题型三反思解决这个类型的题目一般有两种思路:(1)利用“化归”思想将要求的两条平行直线间的距离转化为求其中一条直线上任意一点到另一条直线的距离.(2)直接用公式d=|𝐶1-𝐶2|ට𝐴2+𝐵2,但要注意两直线方程中x,y的系数必须对应相同.题型一题型二题型三解:把l1,l2的方程分别化为l1:3x+4y-10=0,l2:3x+4y-152=0,则l1与l2间的距离d=ฬ-10-൬-152൰ฬට32+42=12.【变式训练2】若例2中l1的方程不变,将l2的方程改为6x+8y=15,求l1与l2间的距离.题...