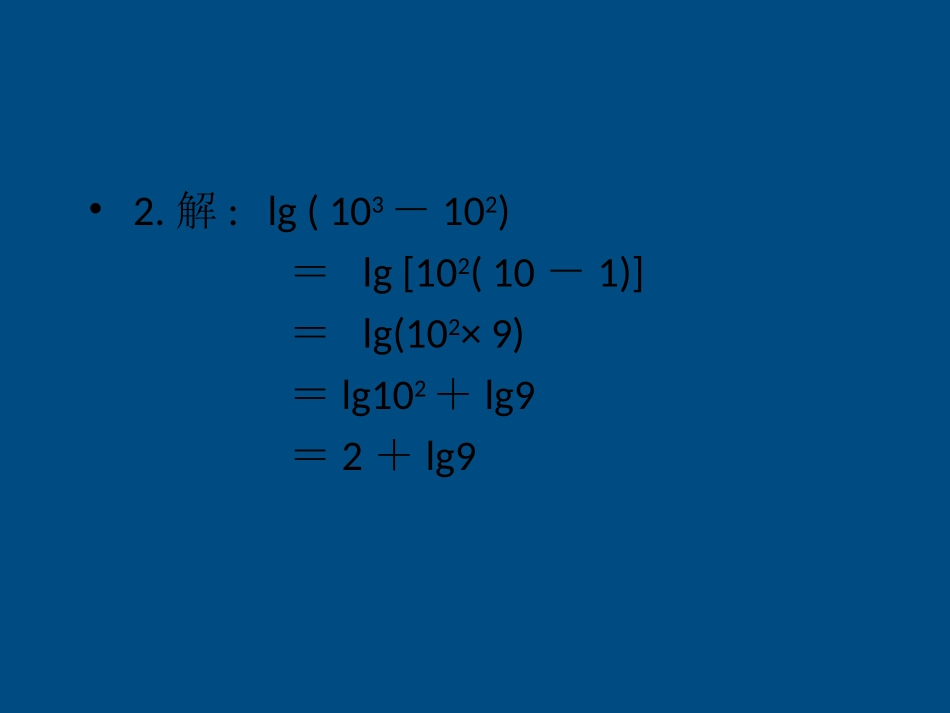高中数学(换底公式)课件1 北师大必修1 课件VIP免费

•练习：1.已知lg2=a,lg3=b,请用a,b表示lg12.2.计算lg(103－102)的结果()。A.1B.C.90D.2＋lg91.解:lg12=lg(4×3)=lg4＋lg3=2lg2＋lg3=2a＋b23•2.解:lg(103－102)＝lg[102(10－1)]＝lg(102×9)＝lg102＋lg9＝2＋lg9（1）18lg7lg37lg214lg3.计算：解法一：18lg7lg37lg214lg18lg7lg)37lg(14lg218)37(714lg201lg)32lg(7lg37lg2)72lg(2)3lg22(lg7lg)3lg7(lg27lg2lg018lg7lg37lg214lg解法二：⑴若lglg2lg3lg,xabc则______x661log12log22⑵的值为______⑶22log843log843_____________提高练习:23abc122•(一)复习•积、商、幂的对数运算法则：•如果a>0，a1，M>0，N>0有：)()()(3R)M(nnlogMlog2NlogMlogNMlog1NlogMlog(MN)loganaaaaaaa证明:设logaN=x,则ax=N，两边取以m为底的对数：从而得：∴aNxmmloglogaNNmmalogloglogNaxNammmxmloglogloglog二、新课：aNNmmalogloglog1.对数换底公式：(a>0,a1，m>0,m1,N>0)①logablogba=1，②（a,b>0且均不为1）1logloglogacbcbabmnbanamloglog2.两个常用的推论:1lglglglgloglogbaababbabmnambnabbamnnamloglglglglglog证：三、讲解范例：例1求log89.log2732的值．一般情况下，可换成常用对数，也可根据真、底数的特征，换成其它合适的底数．分析：利用换底公式统一底数：解：因为log23=a，则,又∵log37=b,∴2log13a1312log7log2log37log42log56log56log33333342babab例3计算：①②3log12.054219432log2log3log例2已知log23=a，log37=b,用a,b表示log425615315555531log3log52.02345412log452log213log21232解：①原式=②原式=例3设且3x=4y=6z1求证；2比较的大小),0(,,zyxzyx1211zyx6,4,3例3设且3x=4y=6z1求证；2比较的大小证明1：设∵∴取对数得：，，∴),0(,,zyxzyx1211zyx6,4,3kzyx643),0(,,zyx1k3lglgkx4lglgky6lglgkzzkkkkkyx1lg6lglg22lg23lg2lg24lg3lg2lg24lglg3lg211例3设且1求证；2比较的大小证明1：设∵∴取对数得：，，∴•2•∴),0(,,zyxzyx643zyx1211zyx6,4,3kzyx643),0(,,zyx1k3lglgkx4lglgky6lglgkzzkkkkkyx1lg6lglg22lg23lg2lg24lg3lg2lg24lglg3lg211kyxlg)4lg43lg3(4304lg3lg8164lglglg4lg3lg81lg64lgkkyx43kzylg)6lg64lg4(6406lg2lg169lglglg6lg2lg64lg36lgkkzy64zyx643∴∴分析：由于x作为真数，故可直接利用对数定义求解；另外，由于等式右端为两实数和的形式，b的存在使变形产生困难，故可考虑将logac移到等式左端，或者将b变为对数形式例4已知logax=logac+b，求x请大家解决。四、小结利用换底公式“化异为同”是解决有关对数问题的基本思想法，它在求值或恒等变形中作了重要作用，在解题过程中应注意：1．针对具体问题，选择好底数．2．注意换底公式与对数运算法则结合使用．3．换底公式的正用与反用．1.已知log189=a,18b=5,用a,b表示log36452.若log83=p,log35=q,求lg53.已知a=(a0),﹥求loga4.计算：（1）log9+log927+()log4（2）7lg20()﹒lg0.732943234116121