高中数学：211(直线的倾斜角和斜率)课件(北师大版必修2) 课件VIP免费

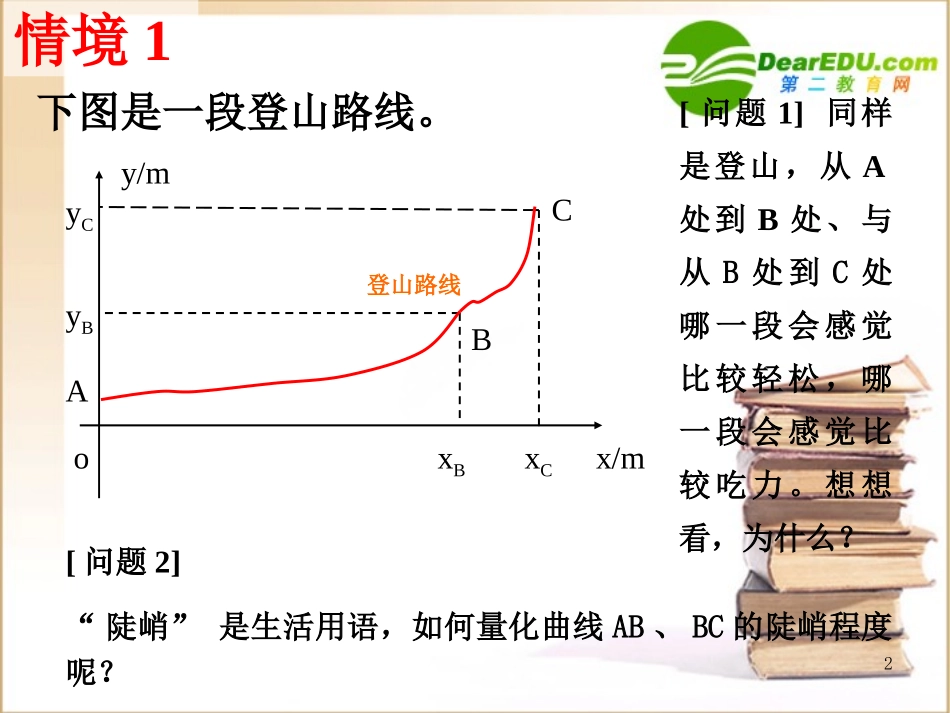
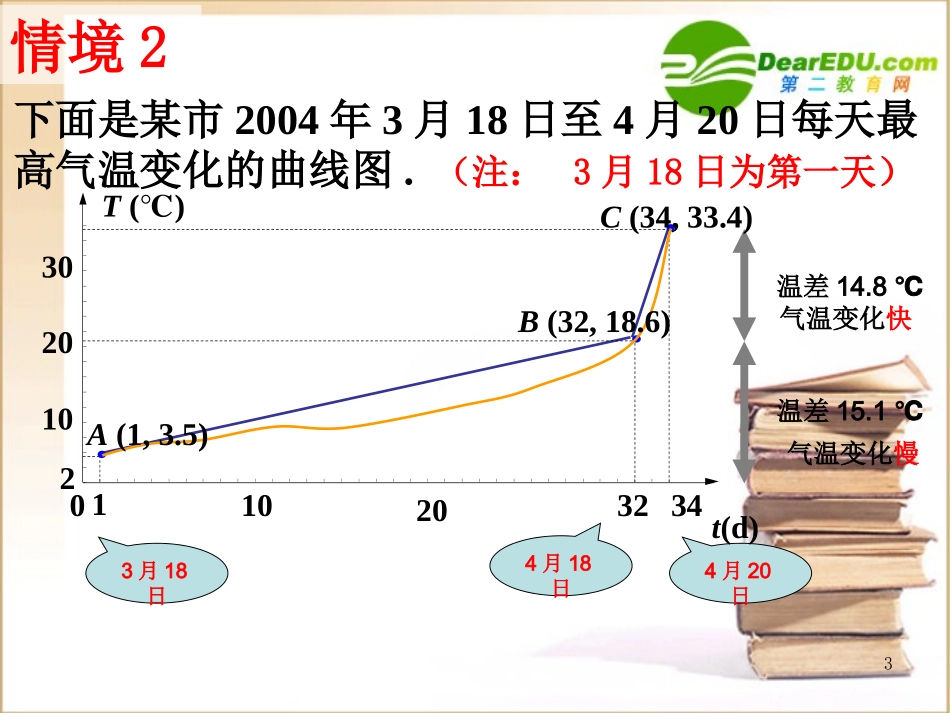
1鹰潭市余江县第一中学：金俊颖变化的快慢与变化率2[问题1]同样是登山，从A处到B处、与从B处到C处哪一段会感觉比较轻松，哪一段会感觉比较吃力。想想看，为什么？y/mx/moxBxCyByC情境1[问题2]“陡峭”是生活用语，如何量化曲线AB、BC的陡峭程度呢？登山路线ABC下图是一段登山路线。3情境2温差15.1℃温差14.8℃3月18日4月18日4月20日气温变化慢气温变化快下面是某市2004年3月18日至4月20日每天最高气温变化的曲线图.（注：3月18日为第一天）t(d)2032342102030A(1,3.5)B(32,18.6)0C(34,33.4)T()℃1104f(x2)－f(x1)x2－x1f(x2)－f(x1)x2－x1对一般的函数y=f(x)来说，当自变量x从x1变为x2时，函数值从yx平均变化率的几何意义：过曲线上A、B两点的直线的斜率.用平均变化率来近似地量化曲线在某区间上的陡峭程度曲线越“陡峭”，变量变化越快;曲线越“平缓”，变量变化越慢.平均变化率的实际意义：在函数值区间[x1，x2]上变化的快慢。f(x1)变为f(x2),它的平均变化率为：yxo)(xfy))(,(22xfxB))(,(11xfxA1x2x某婴儿从出生到第12个月的体重变化如图所示，试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。10.45)/(1035.35.6月kg118.60.4(/)126kg月解:从出生到第3个月,婴儿体重平均变化率为从第6个月到第12个月,婴儿体重平均变化率为应用一T(月)W(kg)639123.56.58.6110从出生到第3个月体重增加得快.6问题：容器甲中水的体积V的平均变化率是一个负数,它的实际意义是什么？甲乙应用二0.13()52(),10ttVtcmV如图，水经过虹吸管从容器甲流向容器乙，秒后甲中水的体积单位：试计算第一个秒内的平均变化率。10V解：在第一个秒内，体积的平均变化率为:3(10)(0)2.550.25(/)10010VVcms10/).Vs3即第一个秒内容器甲中水的体积的平均变化率为-0.25（cm7环保局在规定排污达标日期前，对甲、乙两企业进行检查，其检测结果如图所示（其中W甲(t)、W乙(t)分别表示甲、乙两企业的排污量），试比较两个企业的治污效果。问：在区间上，哪一个企业的排污平均变化率大一些？01tt，WW甲（t）W乙（t）Ot1t标准0t1l2l甲企业好一些乙企业大一些应用三8函数的平均变化率与函数图像有什么联系呢？比较与发现[结论]平均变化率的绝对值越大，曲线越陡峭，变量变化的速度越快。WOt1t0t11t/月W/kg612..03.56.5......38.6..越陡峭，平均变化率越大越陡峭，平均变化率越小甲、乙两人从事某种经营活动所得利润如下图，试比较并评价两人的经营效果.t（月）602425S(万元)乙甲oAB数缺形少直观形缺数难入微应用四10已知函数计算在区间[-3，-1]，[0，5]上及的平均变化率.xxgxxf2)(,12)()(xf)(xg结论：对于一次函数f(x)=kx+b在区间[m，n]上的平均变化率与所给的区间无关，只与一次项系数有关，且其平均变化率为一次项系数。2)3()1()3()1(ff205)0()5(ff解:函数在区间[-3，-1]上的平均变化率为)(xf函数在区间[0，5]上的平均变化率为)(xf函数在区间[-3，-1]上的平均变化率为)(xg2)3()1()3()1(gg)(xg函数在区间[0，5]上的平均变化率为205)0()5(gg一次函数y=kx+b在区间上的平均变化率有什么特点？[m,n](m