高中数学 121 任意角的三角函数3课件 新人教A版必修4 课件VIP免费

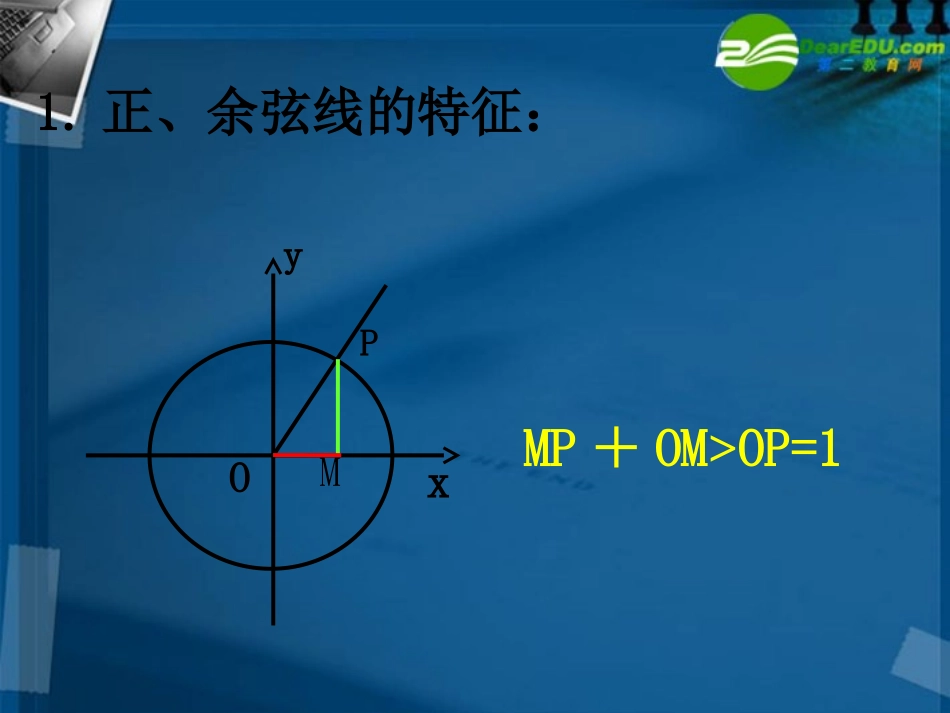
任意角的三角函数（3）第一章三角函数高一年级数学必修41.正、余弦线的特征：POxyMMP＋OM>OP=12.正切线的几何特征过点A（1，0）作单位圆的切线，与角α的终边或其反向延长线相交于点T，则AT=tanα.ATOxyPATOxyP典型例题例1作出下列各角的正弦线、余弦线、正切线：（1）；（2）；（3）；（4）.456231252p2p2p2p例2在0～内，求使成立的α的取值范围.23sin2a>OxyPMP1P232y=例3求函数的定义域.()2cos1faa=-OxyP2MP112x=P任意角的三角函数（4）第一章三角函数高一年级数学必修4湖南师大附中彭萍1.若点P（x，y）为角α终边与单位圆的交点,那么sinα，cosα，tanα对应的函数值分别等于什么？sincostanyxtanyxtanyxtan知识回顾yxP(x，y)Oxy1yx同一个角的正弦、余弦的平方和等于1，商等于这个角的正切.sintancos22sincos122sincos1思考1：对于平方关系可作哪些变形？22sincos122sin1cos,22cos1sin,2(sincos)12sincos,aaaa+=+2(sincos)12sincos,aaaa-=-思考2：对于商数关系可作哪些变形？sintancos理论迁移一、求值:例1(1)已知,求，的值.3sin5costan是第三象限角(2)已知1tan,sin,cos.3求典例分析5sin544sincos例2已知，求的值.分析:平方差公式22sincos144sincos)cos)(sincos(sin222222cossin5sin5由得,,51sin254sin1cos22545153,3tan例3.已知计算:（1）（2）;sin3cos5cos2sin4;cossin典例分析,51cossin,02xxx例4已知计算:;cossinxx（1）（2）.sincoscossin2122xxxx典例分析例5求证:（1）（2）;)cossin1()cos1)(sin1(22（3）;sintansintan2222.cossincossin1cossin2cossin1典例分析1.同角三角函数的两个基本关系是对同一个角而言的，由此可以派生出许多变形公式，应用中具有灵活、多变的特点.2.化简、求值、证明，是三角变换的三个基本问题，具有一定的技巧性，比如平方关系与商的关系的灵活运用，化切为弦、化弦为切以及提公因式法、平方差公式、完全平方公式的运用.课堂小结作业：P21习题1.2A组：10.（1）（2）（3）.11.12