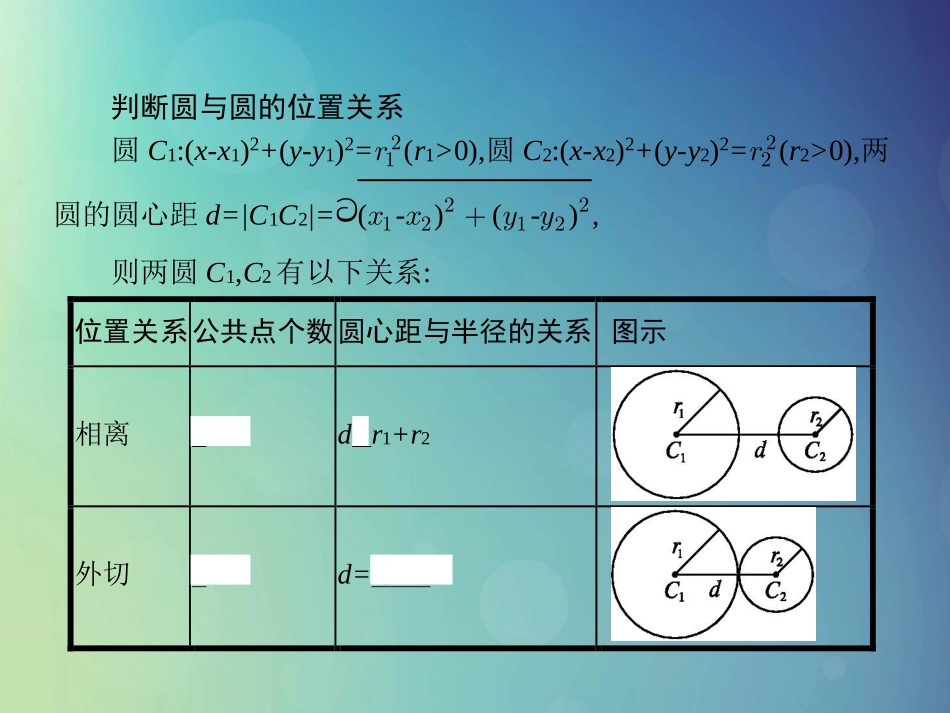
第2课时圆与圆的位置关系1.了解两个圆的位置关系有相离、外切、相交、内切、内含五种情况.2.会根据两圆方程判断两圆的位置关系.3.能利用两圆的位置关系解决相关问题.判断圆与圆的位置关系圆C1:(x-x1)2+(y-y1)2=𝑟12(r1>0),圆C2:(x-x2)2+(y-y2)2=𝑟22(r2>0),两圆的圆心距d=|C1C2|=ට(𝑥1-𝑥2)2+(𝑦1-𝑦2)2,则两圆C1,C2有以下关系:位置关系公共点个数圆心距与半径的关系图示相离0d>r1+r2外切1d=r1+r2位置关系公共点个数圆心距与半径的关系图示相交2|r1-r2|r1+r2.∴圆C1与圆C2相离.两圆的圆心距d=ට(4+1)2+(-2)2=ξ29,题型一题型二题型三题型四题型二两圆相切问题【例2】求与圆x2+y2-2x=0外切且与直线x+ξ3y=0相切于点M(3,-ξ3)的圆的方程.分析:由所求圆和直线x+y=0相切于点M可得到两个条件:(1)圆心和点M的连线与切线垂直;(2)圆心到切线的距离等于圆的半径.又由所求圆与圆x2+y2-2x=0外切可得两圆圆心距与半径之间的等式.考虑设出所求圆的方程,通过待定系数法求解.ξ3题型一题型二题型三题型四解:设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),则ەۖ۔ۖۓට(𝑎-1)2+𝑏2=𝑟+1,𝑏+ξ3𝑎-3=ξ3,|𝑎+ξ3𝑏|2=𝑟,解得൝𝑎=4,𝑏=0,𝑟=2或൝𝑎=0,𝑏=-4ξ3,𝑟=6.故所求圆的方程为(x-4)2+y2=4或x2+(y+4ξ3)2=36.反思处理两圆相切问题,首先必须准确把握是内切还是外切,若只是告诉两圆相切,则必须分两圆内切和两圆外切两种情况讨论;其次根据两圆相切,列出两圆的圆心距与两圆半径之间的关系式.题型一题型二题型三题型四解:方法一:圆O1的圆心坐标为O1(1,2),r1=2ξ5,圆O2的圆心坐标为O2(2,4),r2=ξ5.因为|O1O2|=r1-r2,所以两圆内切,有一条公切线.因为两圆内切,所以直线O1O2与切线垂直,且两圆的公共点即为切点.将两圆方程联立得൜𝑥2+𝑦2-2𝑥-4𝑦-15=0,𝑥2+𝑦2-4𝑥-8𝑦+15=0,解得൜𝑥=3,𝑦=6.【变式训练2】已知圆O1:x2+y2-2x-4y-15=0和O2:x2+y2-4x-8y+15=0,求圆O1,O2的公切线方程.题型一题型二题型三题型四因为直线O1O2的斜率为2,所以切线的斜率为-12,故切线方程为y-6=-12(x-3),即x+2y-15=0.方法二:圆O1的圆心坐标为O1(1,2),r1=2ξ5,圆O2的圆心坐标为O2(2,4),r2=ξ5.因为|O1O2|=r1-r2,所以两圆内切,有一条公切线.将两圆方程联立得ቊ𝑥2+𝑦2-2𝑥-4𝑦-15=0,𝑥2+𝑦2-4𝑥-8𝑦+15=0,①②①-②,得2x+4y-30=0,即x+2y-15=0为所求公切线方程.题型一题型二题型三题型四题型三两圆的公共弦问题【例3】已知两圆x2+y2-2x+10y-24=0和x2+...