高中数学 2-3-2 双曲线的简单几何性质课件2 新人教A版选修2-1 课件VIP免费

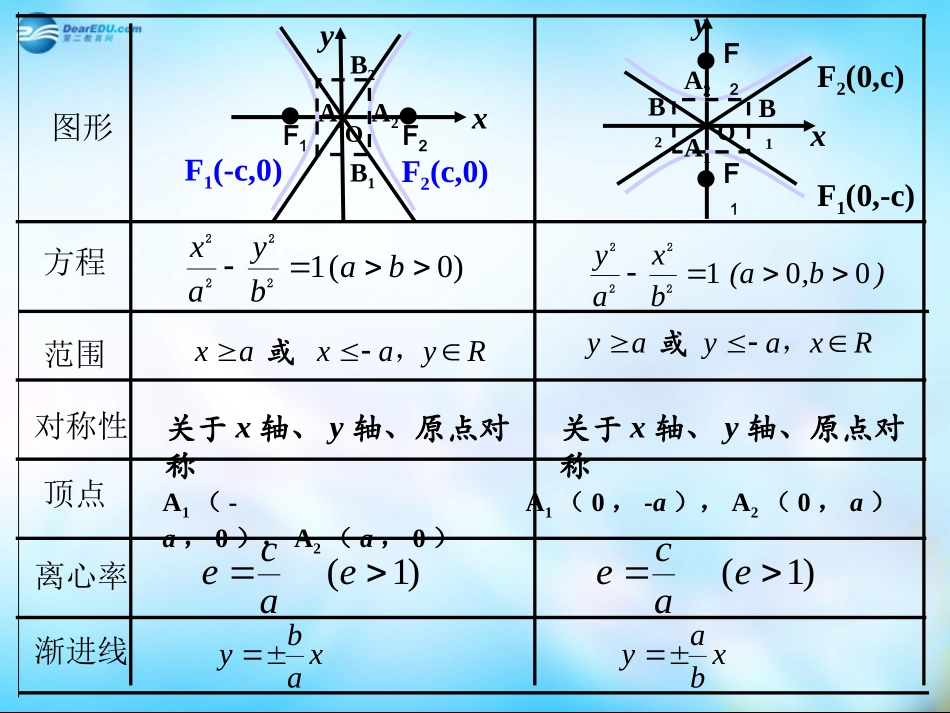
双曲线的性质(二)关于x轴、y轴、原点对称图形方程范围对称性顶点离心率yxOA2B2A1B1..F1F2yB2A1A2B1xO..F2F1)0(1babyax2222bybaxaA1（-a，0），A2（a，0）B1（0，-b），B2（0，b）)10(eaceF1(-c,0)F2(c,0)F1(-c,0)F2(c,0)),b(abyax0012222Ryaxax，或关于x轴、y轴、原点对称A1（-a，0），A2（a，0）)1(eace渐进线无xaby关于x轴、y轴、原点对称图形方程范围对称性顶点离心率)0(1babyax2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）),b(abxay0012222Rxayay，或关于x轴、y轴、原点对称)1(eace渐进线xbay..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)Ryaxax，或)1(eacexaby1、“共渐近线”的双曲线222222221(0)xyxyabab与共渐近线的双曲线系方程为，为参数，λ>0表示焦点在x轴上的双曲线；λ<0表示焦点在y轴上的双曲线。2、“共焦点”的双曲线（1）与椭圆有共同焦点的双曲线方程表示为22221(0)xyabab2222221().xybaab（2）与双曲线有共同焦点的双曲线方程表示为22221(0,0)xyabab2222221()xybaab复习练习：复习练习：1．已知双曲线与椭圆1244922yx共焦点，且以xy34为渐近线，求双曲线方程2．双曲线的中心在原点，焦点在x轴上，两准线间距离为29并且与直线)4(31xy相交所得弦的中点的横坐标是32求这个双曲线方程3．F1、F2是116922xy双曲线的两个焦点,M是双曲线上一点，且3221MFMF求三角形△M的面积1F2F4．一炮弹在A处的东偏北60°的某处爆炸在A处测到爆炸信号的时间比在B处早4秒已知A在B的正东方、相距6千米，P为爆炸地点，（该信号的传播速度为每秒1千米）求A、P两地的距离5．如图，等腰梯形ABCD中|AB|=2|CD|点EAC118所成的比为，双曲线过C、分有向线段D、E三点，且以A、B为焦点求双曲线的离心率ABEDC1244922yx5c1.解析:由椭圆设双曲线方程为12222byax253422baab则16922ba116922yx故所求双曲线方程为2．解析：设双曲线方程为12222byax（a>0，b>0）ca2229 两准线间距离为，∴=2a49ccb4922得c，① 双曲线与直线相交，由方程组)4(3112222xybyax得0)916(98)9(222222abxaxab由题意可知0922ab且32)9(298222221abaxx2297ba②92a72b联立①②解得：所以双曲线方程为17922yx3.解析：由题意可得双曲线的两个焦点是（0，-5）、（0，5），1F2F1F由双曲线定义得：621MFMF联立3221MFMF得21MF22MF221FF+=100=所以△M是直角三角形2F从而其面积为S=162121MFMF4.解析：以直线AB为x轴，线段AB的垂直平分线为y轴，建立直角坐标系，则A（3，0）、B（－3，0）3,5,2614||||cbaPAPB15422yxP是双曲线tan603APkOxyABP右支上的一点 P在A的东偏北60°方向，∴线段AP所在的直线方程为)3(3xy00)3(315422yxxyyx358yx得解方程组即P点的坐标为（8，35）∴A、P两地的距离为22)350()83(AP=10（千米）．OxyABP5.解析：如图，以AB的垂直平分线为y轴，直线AB为x轴，建立直角坐标系，则CDOy⊥ABEDCxy由题意可设A（-c，0），C（2c，h），B（c，0）其中c为双曲线的半焦距，ABc21h是梯形的高由定比分点公式得点E的坐标为cccxE19711812118hhyE19811811180O设双曲线的方程为12222byax由离心率ace点C、E在双曲线上，得.13616436149,14122222222bhacbhac①②由①得1412222acbh代入②得922ac所以离心率322aceyxABEDCO例1、点M（x,y）与定点F（5,0），的距离和它到定直线：的距离的比是常数,求点M的轨迹.l165x5422225)516451169xyxxy（解：由题意得动点M(,)xy与定点(,0)(0)Fcc的距离和它到定直线22()MFxcy,解: 点M(,)xy到定直线2:axc的距离2adxc,依题...