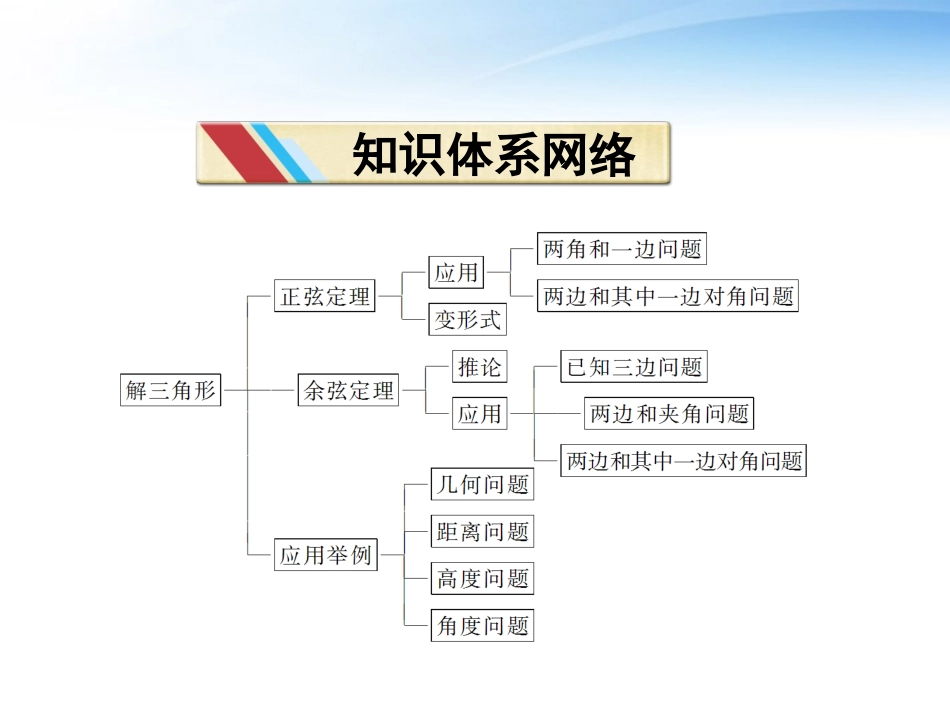
本章优化总结知识体系网络专题探究精讲专题一专题一直接利用正余弦定理求解三角形正弦定理asinΑ=bsinB=csinC=2R体现了三角形中的边角关系,是边与角的和谐统一.正弦定理主要有两方面的应用:一是已知三角形的两个角与任意一边,求其他两边和一角;二是已知三角形的两边与其中一边的对角,求另一边的对角(从而进一步求出其他的边和角).值得注意的是已知三角形的任意两边与其中一边的对角,运用正弦定理解三角形时,解不确定,可结合三角形中大边对大角的性质去判断解的个数.余弦定理有两方面的应用:一是已知三角形的两边和它们的夹角,求第三边和其他两角;二是已知三角形的三边,求三个角.在初中已经学过的勾股定理,它是余弦定理的特例,而余弦定理又可看做是勾股定理的推广,应用中要注意,定理的变式要能够灵活应用.在△ABC中,a=23,b=6,A=30°,求角B及边c.例例11【分析】已知两边及其中一边的对角,用正、余弦定理均能解题.【解】法一:由正弦定理,得sinB=bsinAa=6sin30°23=32.因为a<b,且bsinA=6×12=3<23=b,所以B有两解,得B=60°或120°.当B=60°时,C=90°,c=bsinCsinB=6sin90°sin60°=43;当B=120°时,C=A=30°,所以c=a=23.综上得B=60°,C=43或B=120°,C=23.法二:由余弦定理,得(23)2=62+c2-2×6×c×cos30°,即c2-63c+24=0.所以c=33±3,即c=43或23.当c=43时,cosB=a2+c2-b22ac=12+48-3648=12,所以B=60°,C=90°;当c=23时,a=c=23,所以C=A=30°,所以B=120°.综上得B=60°,C=43或B=120°,C=23.【点评】(1)解斜三角形时,特别要注意已知两边及其中一边对角的情况,此时三角形形状不确定,存在无解、一解、两解三种可能.若用正弦定理,求出某个角的正弦值后,需要讨论是一解、两解还是无解,如法一;若用余弦定理,可化为第三边的方程,用判别式及正根条件来确定是一解、两解还是无解,但法二计算量较法一略大一些.(2)正、余弦定理是解斜三角形的重要依据,但运用哪一个来解是有一定规律的,应加以总结.判定三角形形状通常有两种途径:1.利用正弦定理和余弦定理化边为角(如a=2RsinA,b=2RsinB,c=2RsinC),利用三角变换得出三角形内角之间的关系进行判断,此时应注意一些常见的三角等式所体现的角的关系;2.利用正弦定理、余弦定理化角为边(如sinA=a2R,cosA=b2+c2-a22bc等),通过代数恒等变换,求出三边的关系进行判断.专题二专题二三角形形状的判定在△ABC中,面积S=a2+b2-c24且2sinBsinC=sinA,试判定△ABC的形状.例例22【分析】转化为角或边之间的关系,进而判断.【解】法一:由S=a2+b2-c24,得12absinC=a2+b2-c24.所以2absinC=a2+b2-c2.所以2absinC=2abcosC,所以sinC=cosC.因为C∈(0,π),所以C=π4.由2sinBsinC=sinA得2sinBcosC=sin(B+C),所以sin(B-C)=0.因为-π<B-C<π,所以B-C=0,所以B=C=π4,所以A=π2,即△ABC为等腰直角三角形.法二:由S=a2+b2-c24得2absinC=a2+b2-c2,再由2sinBsinC=sinA及正弦定理得2bsinC=a,所以sinC=a2b.所以a2+b2-c2=2ab·a2b,所以a2+b2-c2=a2,所以b2=c2,所以b=c.再由2absinC=a2+b2-c2=2abcosC,得sinC=cosC,所以C=π4.即B=C=π4,所以A=π2,即△ABC为等腰直角三角形.【点评】三角形形状的判断要从角度或边长之间的关系上来判断,除了应用正余弦定理外,还要注意三角函数中公式的灵活应用和三角函数性质的应用.在解三角形时,有些较复杂的问题常常需要正弦定理、余弦定理交替使用,尽管有时不是直接求出结果,但为了过渡,则必须先求出,至于先用哪个定理,则需具体问题具体分析.专题三专题三正、余弦定理的综合应用在△ABC中,A,B,C相对的边分别为a,b,c,设a,b,c满足条件b2+c2-bc=a2.(1)求A的值;(2)若a=3且b=23cosC,求tanC的值.例例33【分析】由已知条件直接应用余弦定理与正弦定理.【解】(1)由b2+c2-bc=a2,得b2+c2-a2=bc.∴cosA=b2+c2-a22bc=12. 0<A<π,∴A=π3.(2)由bsinB=asinA,∴b=332sinB=2sinB.又 b=23cosC...