高中数学 151 从单位圆看正弦函数的性质课件2(新版)北师大版必修4 课件VIP免费

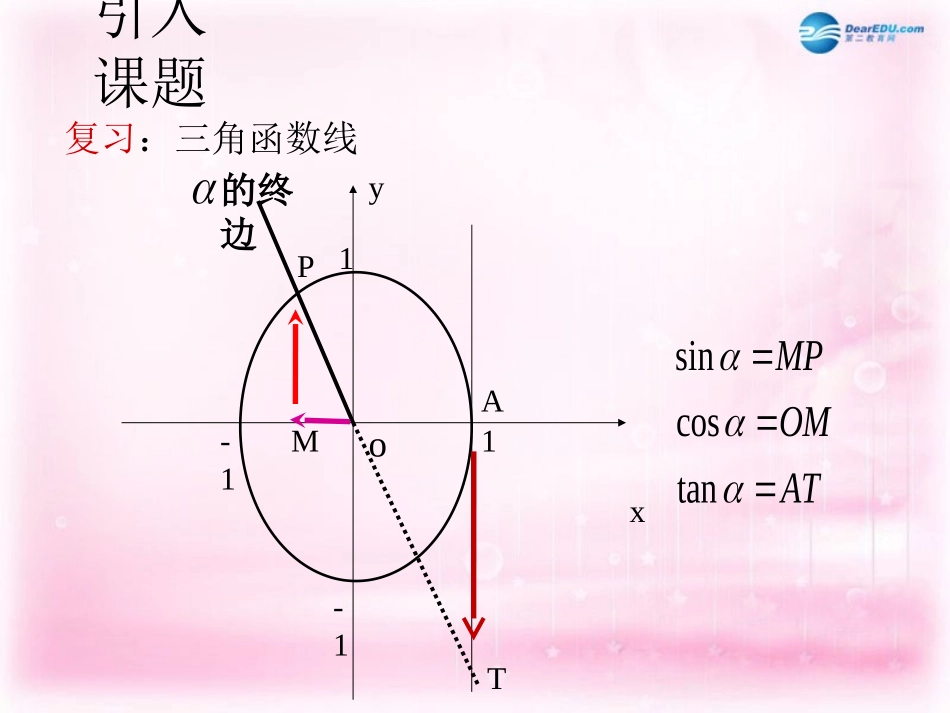
第一章三角函数§5正弦函数的性质与图像第一课时从单位圆看正弦函数的性质学习目标1深入了解三角函数含义2区别正弦函数、余弦函数，并能说出两个函数各自的特点引入课题复习：三角函数线xyoPMT1A的终边-1-11sincostanMPOMAT引入课题•发现：利用单位圆，正弦线、余弦线、正切线分别是正弦、余弦、正切函数的一种几何表示•那么我们应该如何将这种几何表示体现出来探究点11-1022322656723352yx●●●一、正弦函数y=sinx（xR)的图象y=sinx(x[0,])2332346116633265●●●●●●●673435611●●●探究点22oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：探究点2因为终边相同的角的三角函数值相同，所以y=sinx，xR∈的图象在…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2xy---------1-12o46246思考：sin,sin[02]yxxRyxx与，，是相同函数吗？sinyxxR正弦曲线（）探究点3xy1-1cossin()2yxx余弦曲线2余弦函数的图像可以通过正弦曲线向左平移各单位长度而得到．二、余弦函数y=cosx的图象探究点3-oxy---11--13232656734233561126cos[0,2]yxx在函数的图象上，起关键作用的点有：cos,[0,2]yxx最高点：最低点：与x轴的交点：探究点4余弦曲线：cosyxxRxy1-1典例精讲：•观察正弦曲线和余弦曲线，写出满足下列条件x的区间：(1)sin0;x(2)cos0x典例精讲：(1)[02](0,)sin0xx正弦曲线在，内，当时3(2)[02](,)cos022xx余弦曲线在，内，当时(2,2)(xkkkZ)3(2,2)(22xkkkZ)课堂练习3-sin,,22yxx函数的简图是：0sin001,.2DxyxyB解析：选。用特殊点来证明，时，排除选项A，C;又时，排除课堂练习函数f(x)＝sinx＋2|sinx|，x∈[0,2π]的图象与直线y＝k有且仅有两个不同的交点，求k的取值范围．解f(x)＝sinx＋2|sinx|＝3sinx，x∈[0，π]，－sinx，x∈π，2π].图象如图，若使f(x)的图象与直线y＝k有且仅有两个不同的交点，根据上图可得k的取值范围是(1,3)．课堂练习22cos0xx方程的实数解的个数是：解析：（1）作函数y=cosx与函数y=x的图像如图所示，由图像，可知原方程有两个实数解归纳小结1.正弦曲线、余弦曲线特点2.注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]