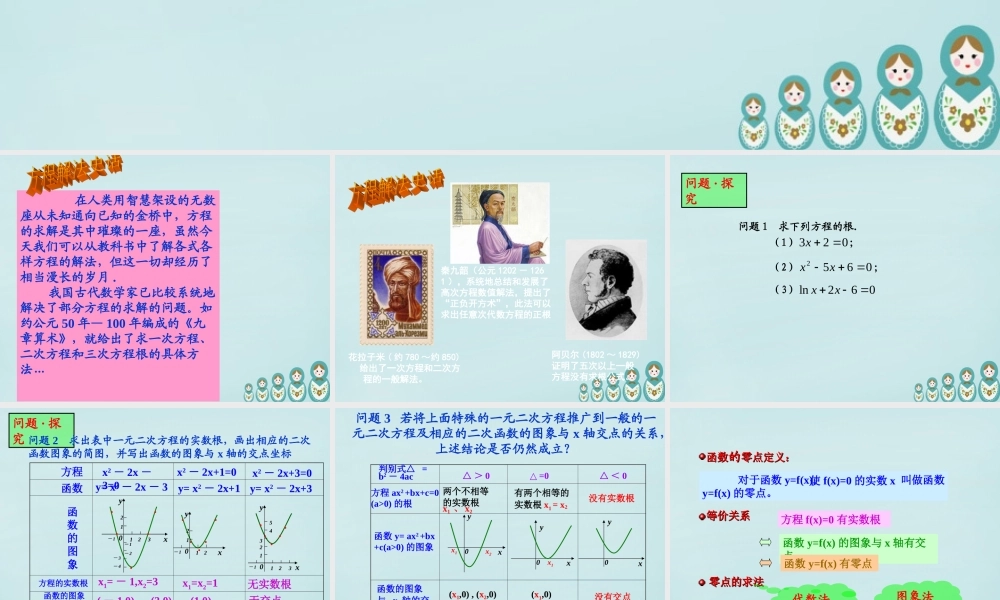
0)(xf)(xfy 在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座,虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月 . 我国古代数学家已比较系统地解决了部分方程的求解的问题。如约公元 50 年— 100 年编成的《九章算术》,就给出了求一次方程、二次方程和三次方程根的具体方法… 花拉子米 ( 约 780 ~约 850)给出了一次方程和二次方程的一般解法。 阿贝尔 (1802 ~ 1829)证明了五次以上一般方程没有求根公式。 秦九韶(公元 1202 - 1261 ),系统地总结和发展了高次方程数值解法,提出了“正负开方术”,此法可以求出任意次代数方程的正根 问题 1 求下列方程的根. (1)023x; (2)0652xx; (3)062ln xx 问题 · 探究 方程x2 - 2x+1=0x2 - 2x+3=0y= x2 - 2x - 3y= x2 - 2x+1函数函数的图象方程的实数根x1= - 1,x2=3x1=x2=1无实数根函数的图象与 x 轴的交点 ( - 1,0) 、 (3,0)(1,0)无交点x2 - 2x -3=0xy0- 132112- 1- 2- 3- 4......... .xy0- 132112543.. . ..yx0- 12112y= x2 - 2x+3问题 · 探究 问题 2 求出表中一元二次方程的实数根,画出相应的二次函数图象的简图,并写出函数的图象与 x 轴的交点坐标方程 ax2 +bx+c=0(a>0) 的根函数 y= ax2 +bx+c(a>0) 的图象判别式△ =b2 - 4ac△ > 0△ =0△ < 0函数的图象与 x 轴的交点有两个相等的实数根 x1 = x2没有实数根xyx1x20xy0x1xy0(x1,0) , (x2,0)(x1,0)没有交点两个不相等的实数根x1 、 x2问题 3 若将上面特殊的一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与 x 轴交点的关系,上述结论是否仍然成立? 对于函数 y=f(x), 叫做函数y=f(x) 的零点。方程 f(x)=0 有实数根函数 y=f(x) 的图象与 x 轴有交点函数 y=f(x) 有零点函数函数的的零点定义:零点定义:等价关系等价关系使 f(x)=0 的实数 x零点的求法 零点的求法 代数法图象法互动交流2 、区别:1 、联系:① 数值上相等:求函数零点就是求方程的根 .② 存在性相同:函数 y=f(x) 有零点 方程 f(x)=0 有实数根 函数 y=f(x) 的图象与 x 轴有交点零点对于函数而言,根对于方程而言.问题 4: 函数的零点与方程的根有什么联系和区别?问题 4: 函数的零点与方程的...