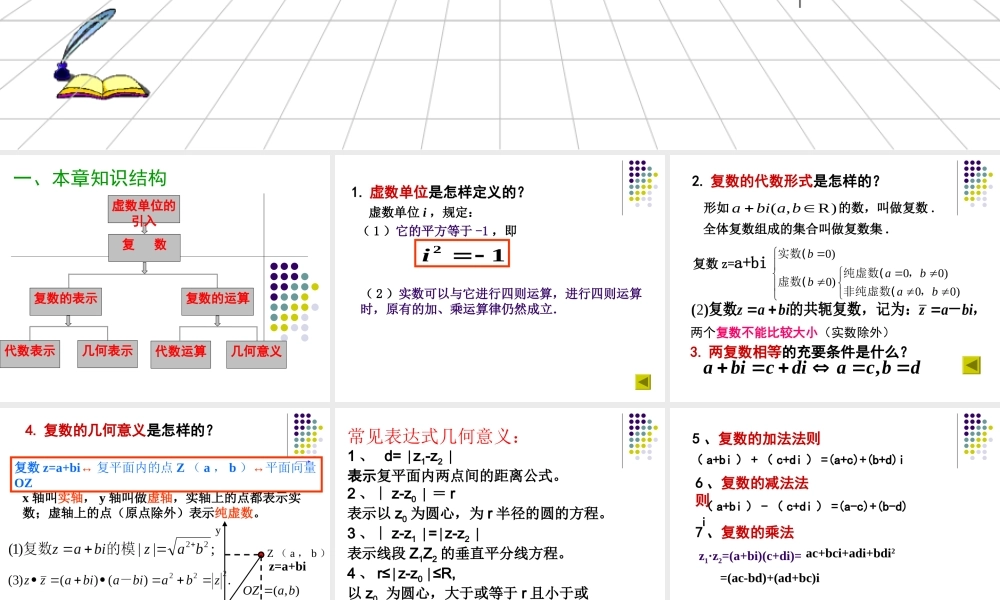
一、本章知识结构虚数单位的引入复 数复数的表示复数的运算代数表示几何表示代数运算几何意义 ( 1 )它的平方等于 -1 ,即12i 1. 虚数单位是怎样定义的?虚数单位 i ,规定:( 2 )实数可以与它进行四则运算,进行四则运算时,原有的加、乘运算律仍然成立. 形如 的数,叫做复数 . )R,(babia2. 复数的代数形式是怎样的?dbcadicbia,3. 两复数相等的充要条件是什么?全体复数组成的集合叫做复数集 .复数 z=a+bi0)00)0)00)babbab实数(纯虚数(,虚数(非纯虚数(,两个复数不能比较大小(实数除外) x 轴叫实轴, y 轴叫做虚轴,实轴上的点都表示实数;虚轴上的点(原点除外)表示纯虚数。4. 复数的几何意义是怎样的?x yOZ ( a , b )z=a+bi( , )OZa b�复数 z=a+bi↔ 复平面内的点 Z ( a , b )↔平面向量OZ 常见表达式几何意义:1 、 d= z∣1-z2 ∣表示复平面内两点间的距离公式。2 、∣ z-z0 ∣ = r表示以 z0 为圆心,为 r 半径的圆的方程。3 、∣ z-z1 = z-z∣ ∣2 ∣表示线段 Z1Z2 的垂直平分线方程。4 、 r≤ z-z∣0 ≤R, ∣以 z0 为圆心,大于或等于 r 且小于或等于 R 的闭圆环。 5 、复数的加法法则6 、复数的减法法则( a+bi ) - ( c+di ) =(a-c)+(b-d)i( a+bi ) + ( c+di ) =(a+c)+(b+d)i7 、复数的乘法z1·z2=(a+bi)(c+di)= ac+bci+adi+bdi2=(ac-bd)+(ad+bc)i 8 、复数的除法))(())((dicdicdicbiadicbia22)(dciadbcbdacidcadbcdcbdac2222 二、基础巩固1 、当 x 为何实数时,复数( 1 )为实数, ( 2 )为虚数 ,( 3 )为纯虚数,( 4 ) Z>0( 5 )对应的 Z 点在第四象限。24 ,zziz 已知求复数2 、4.(09 浙江卷)设1zi ,则22zz 。 ixxxz)32(1223 、 xyO5–5二、典型例题例 1 设复数 z=x+yi(x,y 为实数 ) ,在复平面上的对应点为 Z, 且满足 |z+1-i|=1, 则 |z| 的最值。.变式 1、求22yx 的最值。 变式 2、求 x+y 的最值。 .变式 3、求31xy的最值。 例 2、已知复数满足,2,22虚部为zz Z 所对应的点 A 在第一象限. (1) 求复数 z (2)22,,ZZZZ在复平面上对应点分别为A,B,C.求 ABC的面积 (2) 求ABCcos. (3)求ABCcos. 二...