单纯形法求解VIP免费

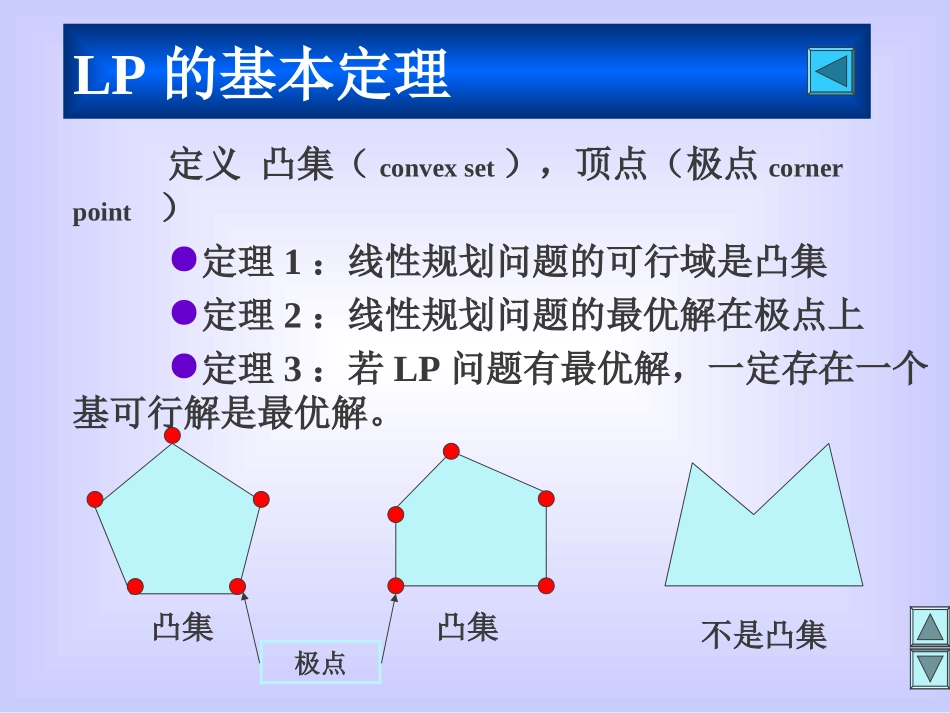
线性规划的基本概念可行解feasiblesolution最优解optimalsolution基basicmatrix(thebasis)基解basicsolution基可行解basicfeasible(BF)solution可行基feasiblebasicmatrix可行域feasibleregionLP的基本定理定义凸集（convexset），顶点（极点cornerpoint）●定理1：线性规划问题的可行域是凸集●定理2：线性规划问题的最优解在极点上●定理3：若LP问题有最优解，一定存在一个基可行解是最优解。凸集凸集不是凸集极点单纯形表基变量miiibCZ10miijijjaCC1C1C2…CmCm+1…Cm+k…CnX1X2…XmXm+1…Xm+k…XnCBXB-Z000…0σm+1…σm+k…σnC1X1b110…0a1m+1…a1m+k…a1nC2X2b201…0a2m+1…a2m+k…a2nCrXrbr00…0arm+1…arm+k…arnCmXmbm00…1amm+1…amm+k…amn……………………………………maxZ=40X1+50X2X1+2X2+X3=303X1+2X2+X4=602X2+X5=24X1…X50（2）列（初始）单纯形表引例用单纯形法求解生产计划问题。解：（1）化标准型4050000X1X2X3X4X5CBXB04050000θ0X33012100150X46032010300X5240200112XB60040000-250X36[1]010-160X4363001-11250X21201001/284000-4001540X161010-10X41800-31[2]950X21201001/2244050000X1X2X3X4X5CBXB04050000θ0X33012100150X46032010300X5240200112XB60040000-250X36[1]010-160X4363001-11250X21201001/284000-4001540X161010-10X41800-31[2]950X21201001/2244050000X1X2X3X4X5CBXB04050000θ0X33012100150X46032010300X5240[2]00112XB60040000-250X36[1]010-160X4363001-11250X21201001/284000-4001540X161010-10X41800-31[2]950X21201001/2244050000X1X2X3X4X5CBXB04050000θ0X33012100150X46032010300X5240[2]00112XB-60040000-250X36[1]010-160X4363001-11250X21201001/2-84000-4001540X161010-10X41800-31[2]950X21201001/2244050000X1X2X3X4X5CBXB04050000θ0X33012100150X46032010300X5240[2]00112XB-60040000-250X36[1]010-160X4363001-11250X21201001/2-84000-4001540X161010-10X41800-31[2]950X21201001/224XB-97500-35/2-15/2040X11510-1/21/200X5900-3/21/2150X215/2013/4-1/40(3)本问题的最优解X=(X1,X2,X3,X4,X5)T=(15,15/2,0,0,9)T且Z=975.X3,X4=0表示资源1，2用完,X5=9表示资源3剩余9.图解分析见下。0(0,0)X2X1ADCB(0,12)(6,12)(15,7.5)从一个基可行解到另一个基可行解单纯形法基本步骤(1)、定初始基，初始基本可行解(3)、若有k>0，Pk全0，停，没有有限最优解；否则转(4)(2)、对应于非基变量检验数j全0。若是，停，得到最优解；若否，转(3)。θ=minaim+k>0=biaim+kbrarm+k定Xr为换出变量，arm+k为主元。由最小θ比值法求：maxj=m+k→Xm+k换入变量j>0(4)、转(2)m+k0…………a1m+k0arm+k1amm+k0初等行变换Pm+k=…………(5)、以arm+k为中心，换基迭代单纯形法的进一步讨论（简介）(一)、大M法theBigMMethod初始基本可行解的求法----------加入人工变量大M使人工变量--------0例：用大M法求解下列问题。maxZ=6X1+4X22X1+3X21004X1+2X2120X1=14X222X1X20解：（1）化标准型maxZ=6X1+4X22X1+3X2+X3=1004X1+2X2+X4=120X1=14X2-X5=22X1…X50（2）加人工变量X6，X7，问题化为maxZ=6X1+4X2-MX6-MX72X1+3X2+X3=1004X1+2X2+X4=120X1+X6=14X2-X5+X7=22X1…X70（3）单纯形求解判定无解条件：当进行到最优表时，仍有人工变量在基中，且≠0，则说明原问题无可行解。原问题maxZ=Cjxjj=1nxj0j=1naijxj=bi(i=1,2,…,m)(二)、两阶段法TheTwo-phaseMethod作辅助问题minW=yii=1mXj，yi0j=1naijxj+yi=bi(i=1,2,…,m)解题过程：第1阶段：解辅助问题当进行到最优表时，①、若W=0,则得到原问题的一个基本可行解，转入第2阶段。②、若W>0,则判定原问题无可行解。第1阶段的任务是将人工变量尽快迭代出去，从而找到一个没有人工变量的基础可行解第2阶段：以第一阶段得到的基础可行解为初始解，采用原单纯型法求解两阶段法原理：(1)、辅助问题的基本可行解X(0)为最优解，对应最小值=0则X(0)的前n个分量是原问题的基本可行解。小结与应用举例小结应用举例(1)、LP数学模型及标准型maxZ=CXAX=b(b0)X0(2)、LP问题解的性质：图解法分析小结(3)、单纯形法：1)、标准型中有单位基。2)、标准型中没有单位基，用大M法加人工变量，使之构成单位基。求maxZ时，目标中－MXj求minZ时，目标中＋MXj3)、判定最优解定理：maxZ问题，检验数j0minZ问题，检验数j04)、解的几种情况：唯一解无穷多解（多重解）无有限最优解（无界解）无可行解多重解–多个解都是最优解，这些解在同一个超平面上，且该平面与目标函数等值面平行–最优单纯型表中有非基变量的检验数为0–最优解的线性组合仍是最优解，即X=aX1+bX2，a+b=1无界解–可行区域不闭合(缺约束条件)–单纯型表中入变量xj*对应的列中所有无可行解–约束条件互相矛盾，无可行域–单纯型表达到最优解检验条件时，人工变量仍在基变量中0*ija