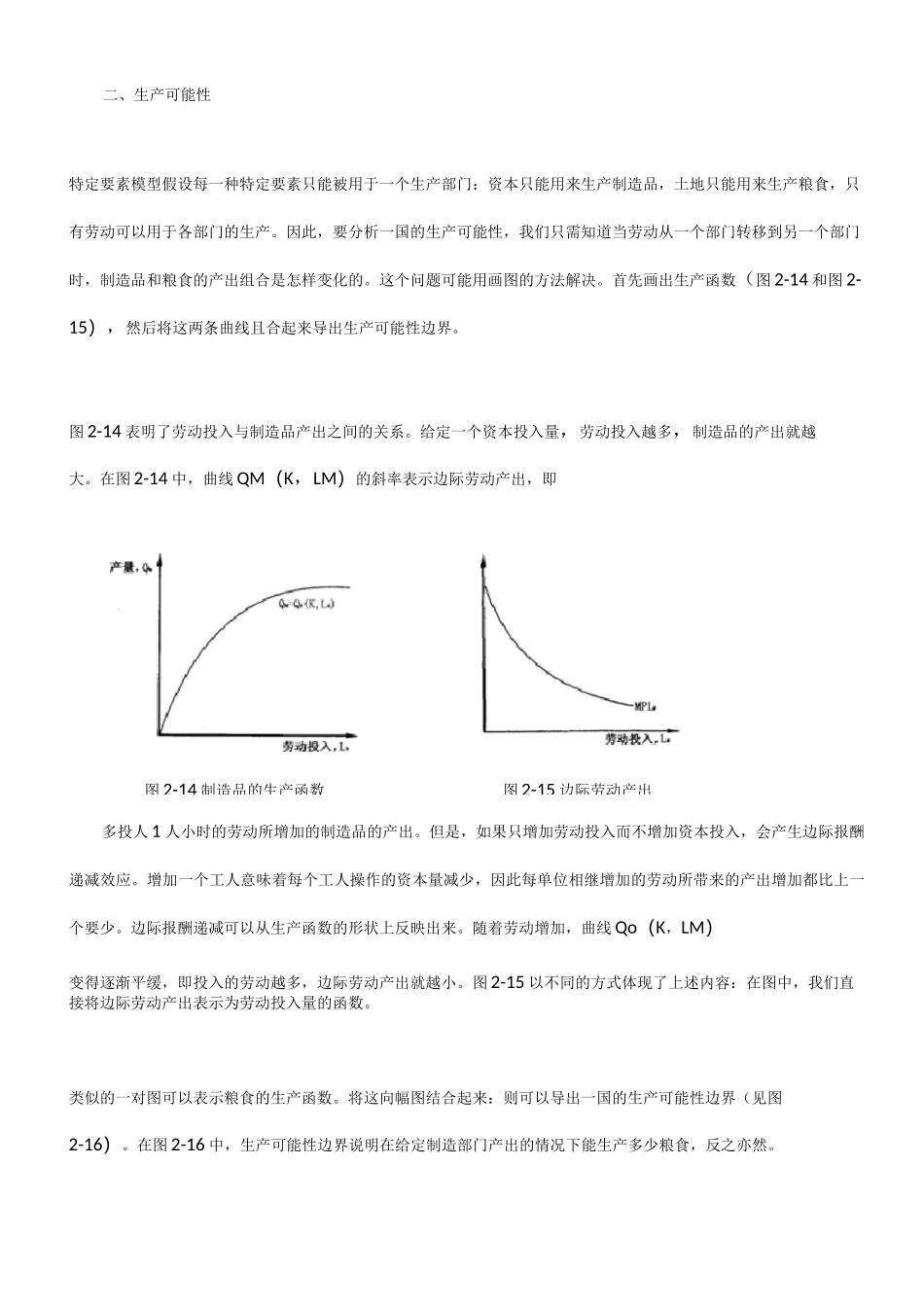
特定要素模型特定要素模型是由保尔•萨缪尔森和罗纳德•琼斯创建发展的。像简单的李嘉图模型一样,特定要素模型假定一个国家生产两种产品,劳动供给可以在两个部门间进行配置。与李嘉图模型不同的是,特定根本模型中存在劳动以外的生产要素。劳动可以在部门间流动,是一种流动要素。其他要素则是特定的,它们只能被用于生产某些特定产品。一、模型的假设设想一个国家能够生产两种产品——制造品和粮食。这个国家有三种生产要素:劳动(L)、资本(K)和土地(T)。生产制造品需要投入劳动和资本,不需要土地。生产粮食需要投入劳动和土地,不需要资本。因此劳动是一种流动要素,每个部门都需要使用劳动。同时,土地和资本都是特定要素,各自只用于一种产品的生产。如何确定每种产品的产量呢?制造品的产出取决于在制造业部门中投入的资本和劳动的多少。产出和投入之间的关系可以用生产函数来归纳。生产函数表明在劳动和资本的投人量一定时制造品的产出量。制造品的生产函数的代数形式为:QM=QM(K,LM)式中,QM 表示制造品的产出,K 表示资本存量,LM 表示在制造品生产中投入的劳动。同样地,粮食的生产函数可以表示为:QF=QF(T,LF)式中,QF 表示粮食的产出,T 表示土地的供给量,LF 表示在粮食生产中投入的劳动。从国家整体上来说,各部门投入的劳动之和等于总的劳动供给量 L:LM+LF=L图 2-15 边际劳动产出二、生产可能性特定要素模型假设每一种特定要素只能被用于一个生产部门:资本只能用来生产制造品,土地只能用来生产粮食,只有劳动可以用于各部门的生产。因此,要分析一国的生产可能性,我们只需知道当劳动从一个部门转移到另一个部门时,制造品和粮食的产出组合是怎样变化的。这个问题可能用画图的方法解决。首先画出生产函数(图 2-14 和图 2-15),然后将这两条曲线且合起来导出生产可能性边界。图 2-14 表明了劳动投入与制造品产出之间的关系。给定一个资本投入量,劳动投入越多,制造品的产出就越大。在图 2-14 中,曲线 QM(K,LM)的斜率表示边际劳动产出,即多投人 1 人小时的劳动所增加的制造品的产出。但是,如果只增加劳动投入而不增加资本投入,会产生边际报酬递减效应。增加一个工人意味着每个工人操作的资本量减少,因此每单位相继增加的劳动所带来的产出增加都比上一个要少。边际报酬递减可以从生产函数的形状上反映出来。随着劳动增加,曲线 Qo(K,LM)变得逐渐平缓,即投入的劳动越多,边际劳动产出就越小。...