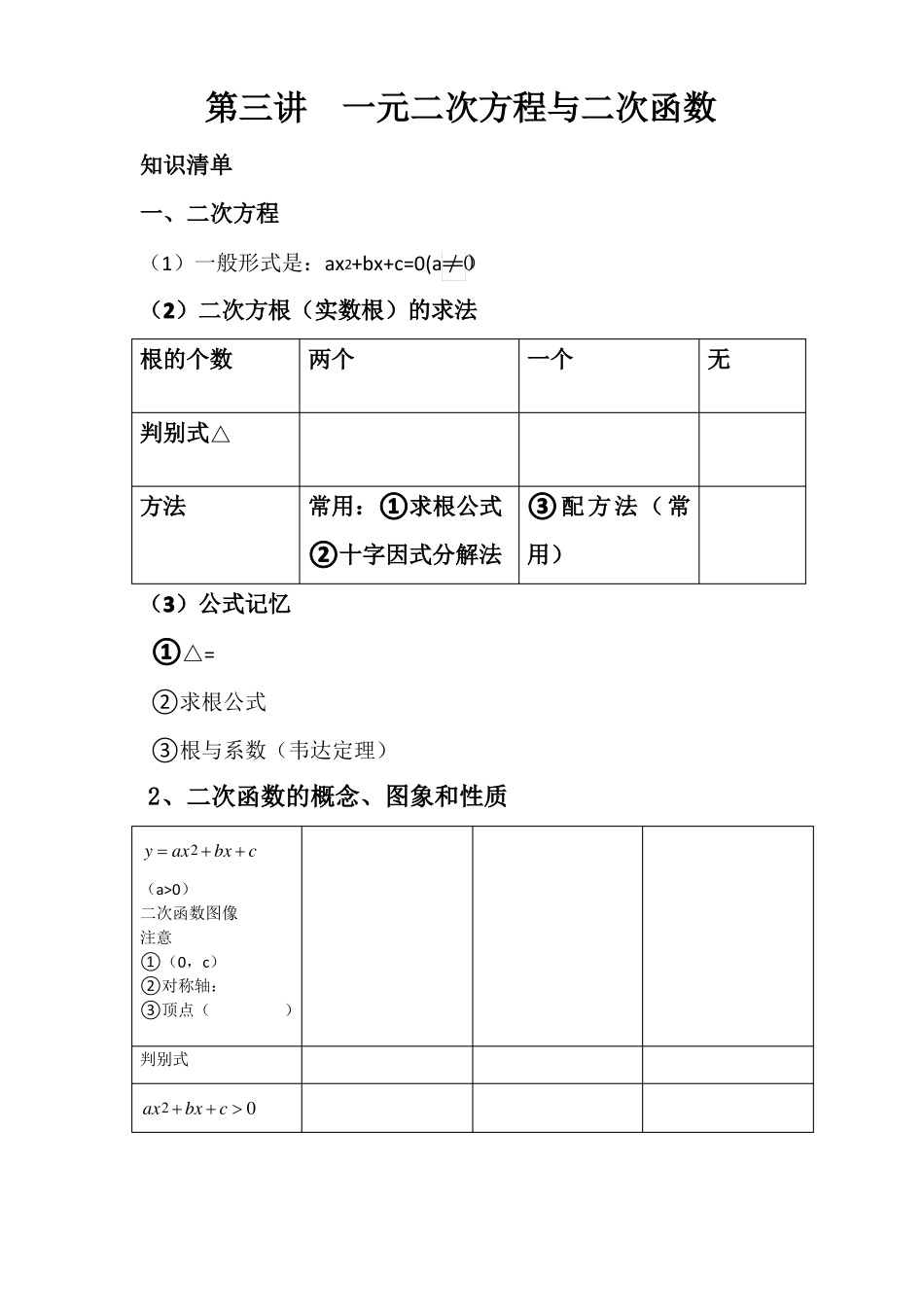
第三讲一元二次方程与二次函数知识清单一、二次方程(1)一般形式是:ax2+bx+c=0(a≠0)(2)二次方根(实数根)的求法根的个数判别式△方法两个一个无常用:①求根公式③配方法(常②十字因式分解法用)(3)公式记忆①△=②求根公式③根与系数(韦达定理)2、二次函数的概念、图象和性质y ax2 bx c(a>0)二次函数图像注意①(0,c)②对称轴:③顶点()判别式ax bx c 02二次不等式口诀:二次函数的形式:①一般式:②顶点式:③两根式:问题一:二次方程根的求法例 1:用适当的方法解方程:(1)2(x+2)2-8=0(2)x(x-3)=x(3) 3 x2=6x- 3(4)(x+3)2+3(x+3)-4=0点评:写出每个分解的方法变式 1:判定下列关于 x 的方程的根的情况(其中 a 为常数),如果方程有实数根,写出方程的实数根。(1)x2-3x+3=0;(2)x2-ax+(a-1)=0;点评:当二次方程系数含参数求根时,需注意什么:________问题二:韦达定理的应用例 2:已知方程 5x2+kx-6=0 的一个根是 2,求它的另一个根及k 的值。点评:要用两种以上的方法求解:变式 1:已知关于 x 的方程 x2+2(m-2)x+m2+4=0 有两个实数根,并且这两个实数根的平方和比两个根的积大于 21,求 m 的值。变式 2:.若 x1,x2是方程 x2+2x-2007=0 的两个根,试求下列各式的值:2(1) x12+ x2 ;(2) 11+;x1x2(3)(x1-5)(x2-5);(4) x1 x2 .问题三:二次函数解析式的求法例 3:已知某二次函数的最大值为 2,图象的顶点在直线 y=x+1 上,并且图象经过点(3,-1),求二次函数的解析式。变式 1、已知二次函数的图象过点(-3,0),(1.0),且顶点到 x 轴的距离等于 2,求此二次函数的表达式。变式 2、已知二次函数的图像过点 (1,22),(0,8),(2,8) ,求此函数的表达式变式 3、把二次函数 y=x2+bx+c 的图象向上平移 2 个单位长度,再向左平移 4 个单位长度,得到函数 y=x2的图象,求 b,c 的值。点评:当选择二次函数解析式的形式时,应该注意的条件式什么。请总结:问题 4、二次函数最值的应用例 4:当 x≥0 时,求函数 y=-x(2-x)的取值范围。变式 1:当 1≤x≤2 时,求函数 y=-x2-x+1 的最大值和最小值。变式 2(拓展):当 t≤x≤t+1 时,求函数 y=x2 x 的最小值(其中 t 为常数)。1252问题 5、二次不等式的求解例 5:已知二次函数 y=x2-x-6,当取 x 何值时,y=0?当取 x 何值...