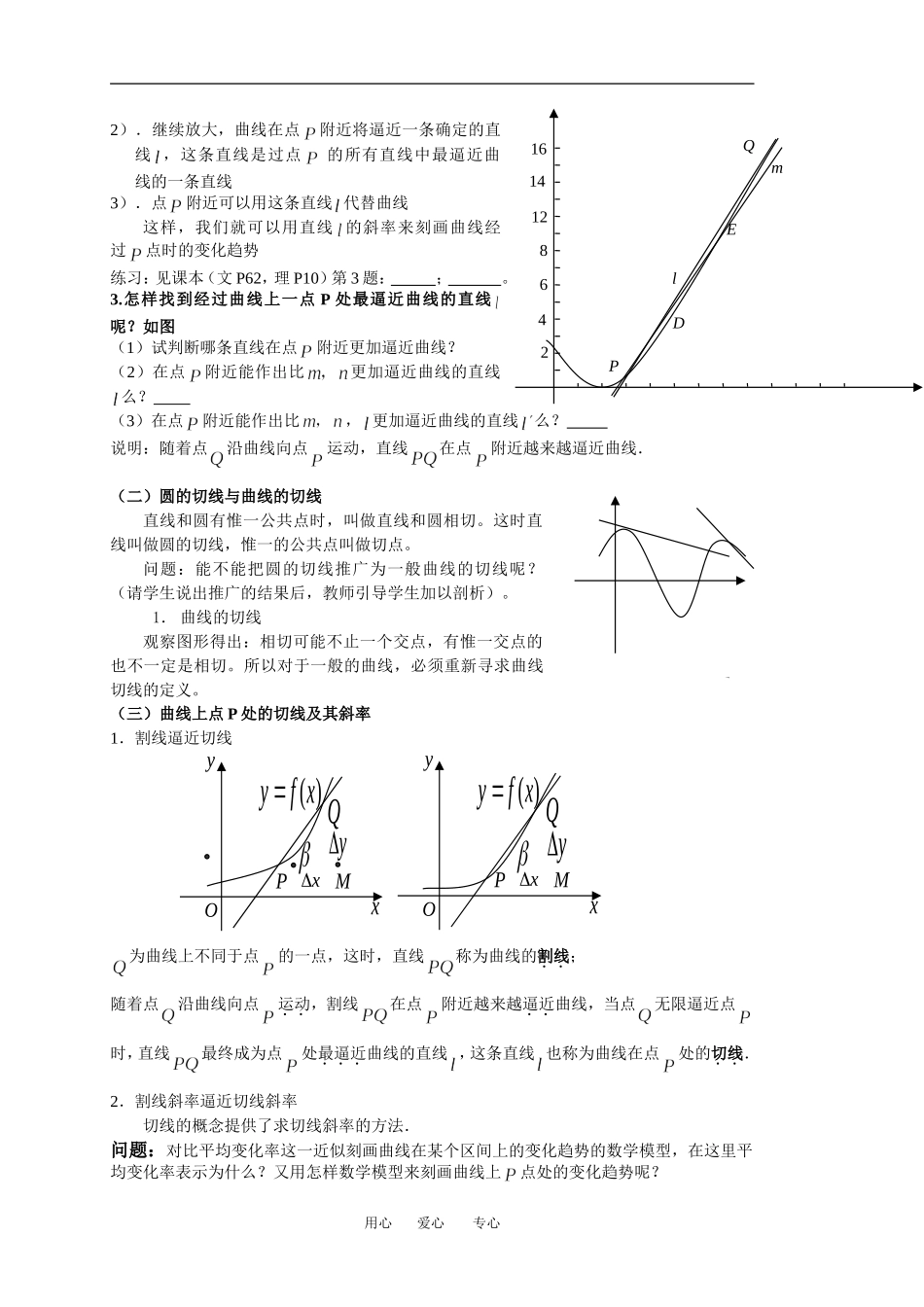
1.1.2 瞬时变化率-导数(一)曲线上一点处的切线一、教学目标1.理解并掌握曲线在某一点处的切线的概念 2.掌握用割线逼近切线的方法.3.会求曲线在一点处的切线的斜率与切线方程,二、问题情景导数是解决函数的最大值、最小值问题的有力工具.导数的知识形成一门学科,就是我们通常所说的微积分.微积分除了解决最大值、最小值问题,还能解决一些复杂曲线的切线问题.导数的思想最初是法国数学家费马(Fermat)为解决极大、极小问题而引入的.但导数作为微分学中最主要概念,却是英国科学家牛顿(Newton)和德国数学家莱布尼兹(Leibniz)分别在研究力学与几何学过程中建立的.微积分能成为独立的科学并给整个自然科学带来革命性的影响,主要是靠了牛顿和莱布尼兹的工作.但遗憾的是他们之间发生了优先权问题的争执.其实,他们差不多是在相同的时间相互独立地发明了微积分.方法类似但在用语、符号、算式和量的产生方式稍有差异.牛顿在 1687 年以前没有公开发表,莱布尼兹在 1684 年和 1686 年分别发表了微分学和积分学. 所以,就发明时间而言,牛顿最于莱布尼兹,就发表时间而言,莱布尼兹则早于牛顿.关于谁是微积分的第一发明人,引起了争论.而我们现在所用的符号大多数都是莱布尼兹发明的.而英国认为牛顿为第一发明人,拒绝使用莱布尼兹发明的符号,因此,使自己远离了分析的主流奎屯王新敞新疆三、教学过程(一)点附近的曲线1.平均变化率:函数在区间上的平均变化率为 .即曲线上两点的连线(割线)的斜率。显然平均变化率近似地刻画了曲线在某个区间上的变化趋势。2.如何精确地刻画曲线上某一点处的变化趋势呢?(点附近的曲线的研究)(从直线上某点的变化趋势的研究谈起,结合“天圆地方”的故事带来“宏观上曲,微观上直”,“曲绝对,直相对”的初步感受,后提出“放大图形”的朴素方法.)(1)观察“点附近的曲线”,随着图形放大,你看到了怎样的现象? (2)这种现象下,这么一条特殊位置的曲线从其趋势看几乎成了 这种思维方式就叫做“逼近思想”。从上面的学习过程来看:1).曲线在点附近看上去几乎成了直线用心 爱心 专心放大P放大PP放大P放大PP2).继续放大,曲线在点附近将逼近一条确定的直线 ,这条直线是过点 的所有直线中最逼近曲线的一条直线3).点附近可以用这条直线 代替曲线这样,我们就可以用直线 的斜率来刻画曲线经过点时的变化趋势练习:见课本(文 P62,理 P10)第 3 题: ; 。3.怎样找到经过曲...