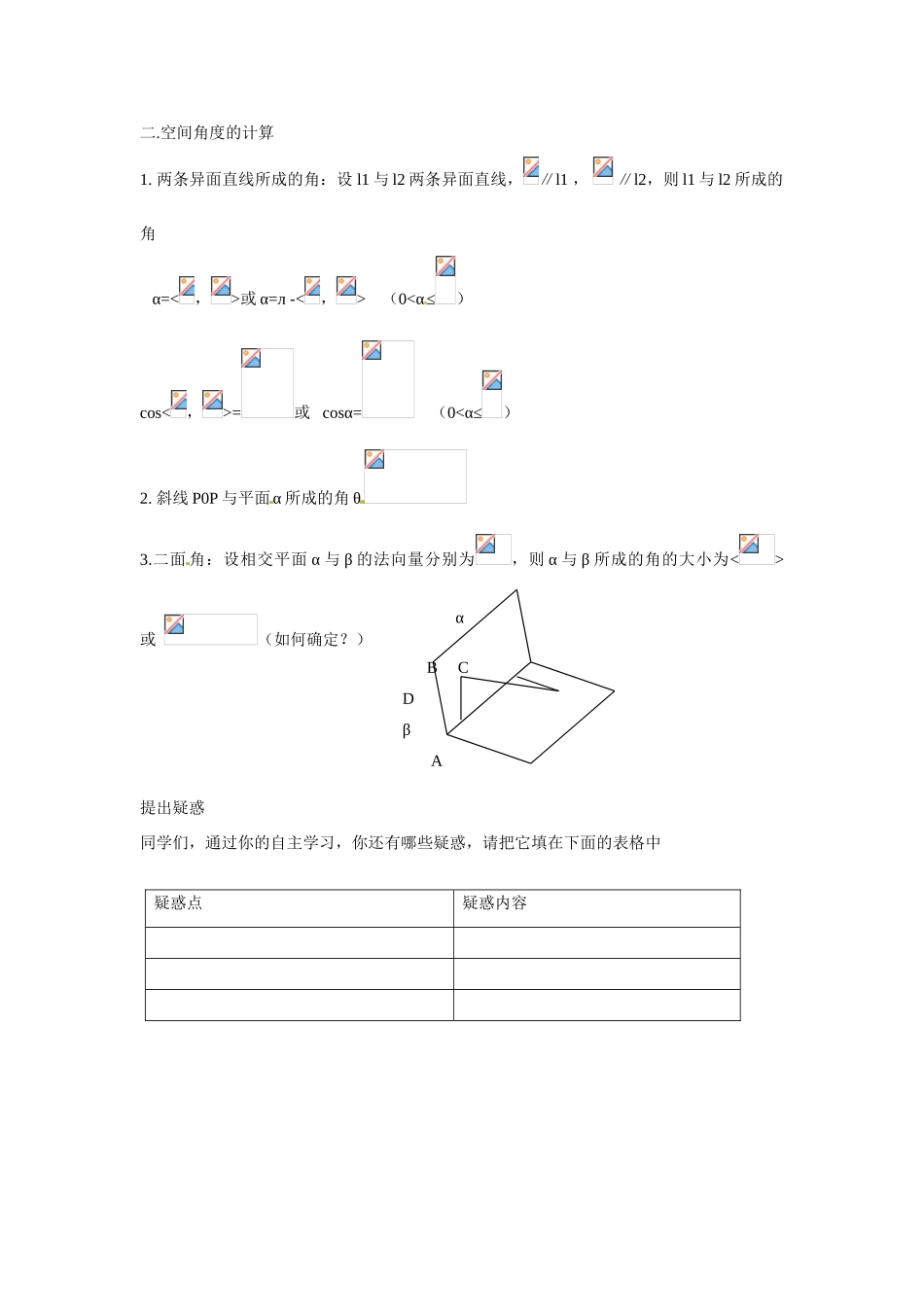
3.2 立体几何中的向量方法课前预习学案预习目标:向量的相关知识:概念、基本运算、建系方法、坐标求法(不定点的坐标)、平行与垂直法向量求法向量作为工具解决立几问题的方法预习内容:一.空间距离的计算1. 空间两点间的距离:设 A、B 是空间两点,则 A、B 两点间的距离 2.两条异面直线间的距离:设 a、b 是两条异面直线,是 a、b 的公共法向量(即),点 Aa,Bb则异面直线 a、b 间的距离 即方向上的射影长为异面直线 a、b 间的距离。3.点(或线)到平面的距离:1)设P 是平面 α 内任一点,则 PO 到 平面 α 的距离2)直线与平面(或平面与平面)的距离转化为点到平面的距离。 abnABdPαP0dOθβ二.空间角度的计算1. 两条异面直线所成的角:设 l1 与 l2 两条异面直线,∥l1 , ∥l2,则 l1 与 l2 所成的角 α=<,>或 α=л -<,> (0<α≤)cos<,>=或 cosα= (0<α≤)2. 斜线 P0P 与平面α 所成的角 θ3.二面 角:设相交平面 α 与 β 的法向量分别为,则 α 与 β 所成的角的大小为<> 或 (如何确定?)提出疑惑同学们,通过你的自主学习,你还有哪些疑惑,请把它填在下面的表格中疑惑点疑惑内容 α B CD β A 课内探究学案学习目标:1 掌握好向量的相关知识:概念、基本运算、建系方法、 坐标求法(不定点的坐标)、平行与垂直、法向量求法1 掌握向量作为工具解决立几问题的方法重点难点:向量作为工具解决立几问题的方法学习过程:例 1.在棱长为 1 的正方体中,E、F 分别是的中点,G 在棱CD 上,且,H 为 C1G 的中点,应用空间向量方法求解下列问题。(1)求证:EF⊥B1C;(2)求 EF 与 C1G 所成的角的余弦;(3)求 FH 的长。例 2.如图,在棱长为 2 的正方体中,E 是 DC 的中点,取如图所示的空间直角坐标系。(1)写出 A、B1、E、D1 的坐标;(2)求 AB1 与 D1E 所成的角的余弦值。例 3. 如 图 , 在 四 棱 锥中 , 底 面 ABCD 是 正 方 形 , 侧 棱 PD⊥ 底 面 ABCD,PD=DC,E 是 PC 的中点,作 EF⊥PB 交 PB 于点 F。(1)证明 PA//平面 EDB;(2)证明 PB⊥平面 EFD;(3)求二面角 C—PB—D 的大小。当堂检测:1、如图,已知矩形 ABCD 所在平面外一点 P,PA⊥平面 ABCD,E、F 分别是 AB、PC 的中点。(1)求证:EF//平面 PAD;(2)求证:EF⊥CD;(3)若,求 EF 与平面 ABCD...