高中数学 第一章 三角函数 阶段复习课 第2课 三角函数的图象与性质及其应用学案 新人教A版必修4-新人教A版高一必修4数学学案

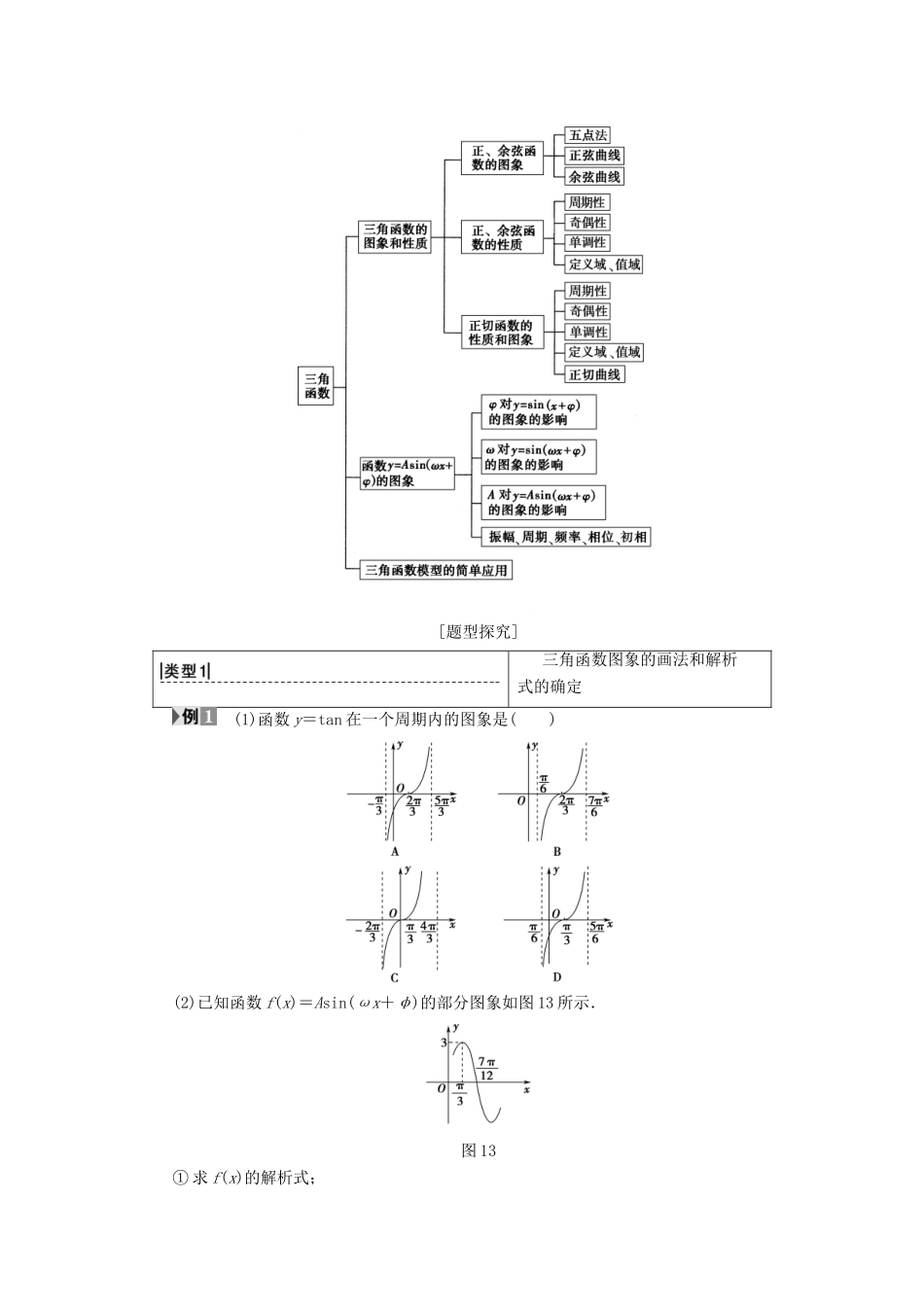
第二课 三角函数的图象与性质及其应用[核心速填]1．三角函数的性质(1)正弦函数：定义域为 R，值域为[ － 1,1] ，奇函数，单调增区间：(k∈Z)；单调减区间：(k∈Z)(2)余弦函数：定义域为 R，值域为[ － 1,1] ，偶函数，单调增区间： [－π＋2kπ，2kπ](k∈Z)；单调减区间：[2kπ，π＋2kπ](3)正切函数：定义域为；值域为 R，奇函数，单调增区间：2．函数 y＝Asin(ωx＋φ)的图象及简单应用A，ω，φ 对函数 y＝Asin(ωx＋φ)图象的影响．(1)φ 对 y＝sin(x＋φ)，x∈R 的图象的影响：(2)ω(ω＞0)对 y＝sin(ωx＋φ)的图象的影响：(3)A(A＞0)对 y＝Asin(ωx＋φ)的图象的影响：[体系构建][题型探究]三角函数图象的画法和解析式的确定 (1)函数 y＝tan 在一个周期内的图象是( )(2)已知函数 f(x)＝Asin(ωx＋φ)的部分图象如图 13 所示．图 13① 求 f(x)的解析式；② 请写出 g(x)＝f 的表达式，并求出函数 y＝g(x)的图象的对称轴和对称中心. 【导学号：84352150】(1)A [(1)y＝tan 的周期 T＝＝2π，排除 B，D当 x＝0 时，tan＝－.故选 A.](2)① 由图可知 A＝3，＝－，∴T＝π⇒ω＝2，f(x)＝3sin(2x＋φ)，∴＋φ＝，φ＝－，∴f(x)＝3sin.② 由(1)知 g(x)＝f＝3sin＝3sin＝3cos 2x，令 2x＝kπ(k∈Z)，∴所求的对称轴为直线 x＝(k∈Z)，令 2x＝＋kπ(k∈Z)，x＝＋(k∈Z)，∴所求的对称中心为(k∈Z)．[规律方法] 1“五点法”作图中的五点分别为图象的最高点、最低点及与 x 轴的交点，描点作图并向左或向右平移即得正弦曲线和余弦曲线.2 y＝sin x 的图象的对称轴方程为 x＝kπ＋，k∈Z，对称中心为kπ，0，k∈Z，y＝cos x 的图象的对称轴方程为 x＝kπ，k∈Z，对称中心为，k∈Z，y＝tan x 的图象的对称中心为，k∈Z.3 由已知条件确定函数 y＝Asinωx＋φ的解析式，需要确定 A，ω，φ，其中 A，ω 易求，下面介绍求 φ 的几种方法.① 平衡点法由 y＝Asinωx＋φ＝Asin 知它的平衡点的横坐标为－，所以我们可以找与原点相邻的且处于递增部分的平衡点，令其横坐标为 x1＝－\f(φ,ω)，则可求 φ.② 确定最值法这种方法避开了“伸缩变换”且不必牢记许多结论，只需解一个特殊的三角方程.③ 利用单调性将函数 y＝Asinωx＋φ的图象与 y＝sin x 的图象比较，选取它们的某一个单调区间得到一个等式，解答即可求出 φ. [...