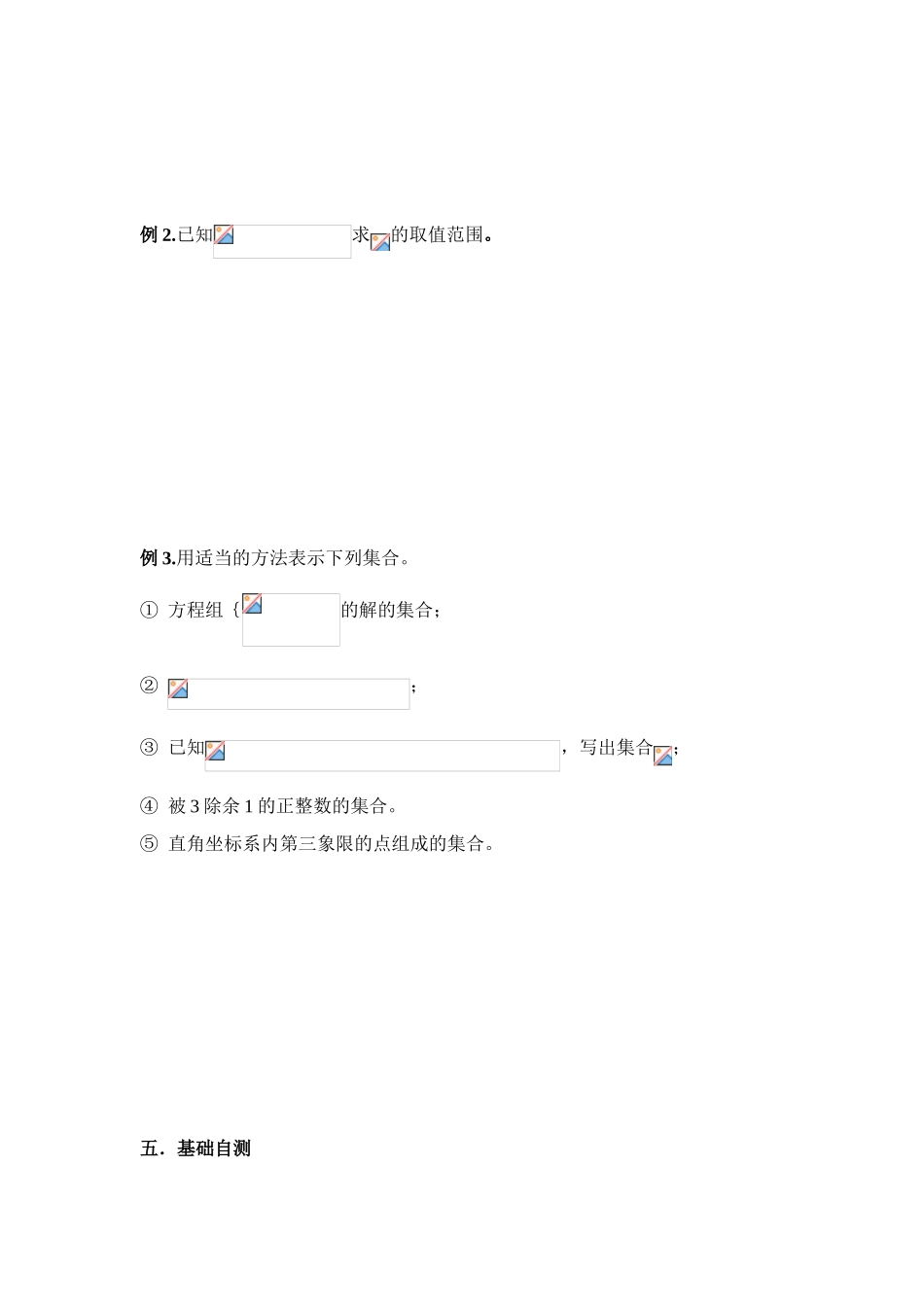
§1.1.1 集合的含义与表示 一. 教学目标: l.知识与技能(1)通过实例,了解集合的含义,体会元素与集合的属于关系;(2)知道常用数集及其专用记号;(3)了解集合中元素的确定性.互异性.无序性;(4)会用集合语言表示有关数学对象;(5)培养学生抽象概括的能力.2. 过程与方法 (1)让学生经历从集合实例中抽象概括出集合共同特征的过程,感知集合的含义.(2)让学生归纳整理本节所学知识.3. 情感.态度与价值观使学生感受到学习集合的必要性,增强学习的积极性.二. 教学重点.难点重点:集合的含义与表示方法.难点:表示法的恰当选择.三.基础知识梳理1.元素与集合的概念(1)把_____________________统称为元素,通常用________________________表示。(2)把__________________________叫做集合(简称为集),通常用____________表示。2.集合中元素的特性(1)确定性:给定集合,它的元素必须是____________。(2)互异性:一个给定集合中的元素是____________。(3)无序性:集合中的元素是________________________如与时同一集合。3.集合相等只要_____________________________________就称这两个集合是相等的。4.元素与集合之间的关系(1)如果是集合的元素,就说__________________,记作__________________.(2)如果不是集合的元素,就说________________,记作__________________. 5.常用数集及表示符号 名称 非负整数集( 自 然 数集)正整数集整数集有理数集实数集符号6.集合的表示方法集合除了用自然语言描述外,还可以用__________和__________表示。列举法把集合的元素__________出来,并用大括号括起来表示集合的方法。描述法用______________________________表示集合的方法。四.例题分析例 1.考察下列每组对象能否构成一个集合。① 美丽的小鸟②不超过 20 的非负数③立方接近零的正数④直角坐标系中,第一象限内的点。例 2.已知求的取值范围。例 3.用适当的方法表示下列集合。① 方程组{的解的集合;②;③ 已知,写出集合;④ 被 3 除余 1 的正整数的集合。⑤ 直角坐标系内第三象限的点组成的集合。五.基础自测1.下列各条件中能够成集合的是( )(A)世界著名科学家(B)在数轴上与原点非常近的点(C)所有等腰三角形(D)全班成绩好的同学2.已知集合 S 中三个元素是的三边长,那么一定不是( )(A)锐角三角形 (B)直角三角形(C)钝角三角形 (D)等腰三角形 3.给出下列几个关系正确的有几个( ...