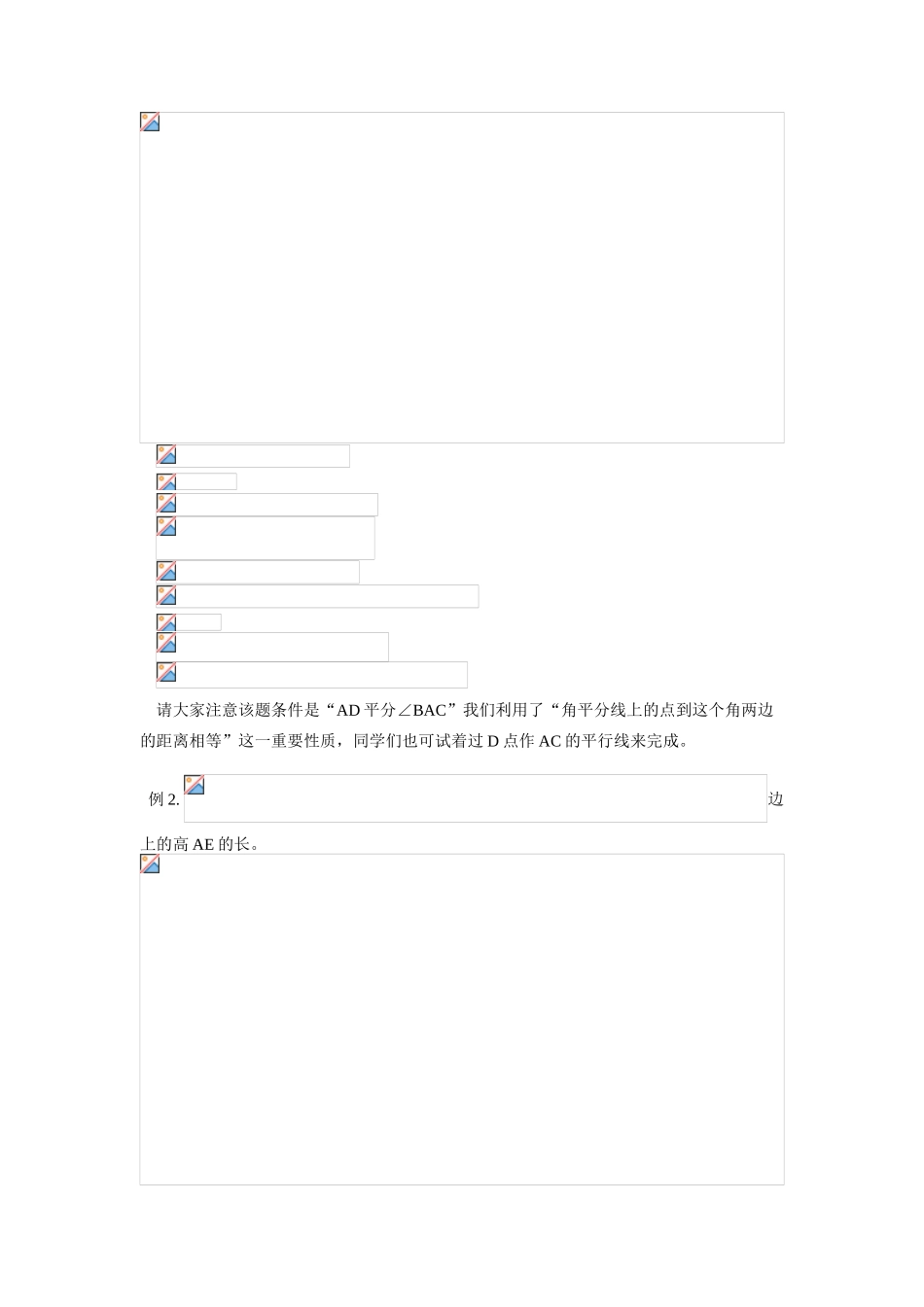
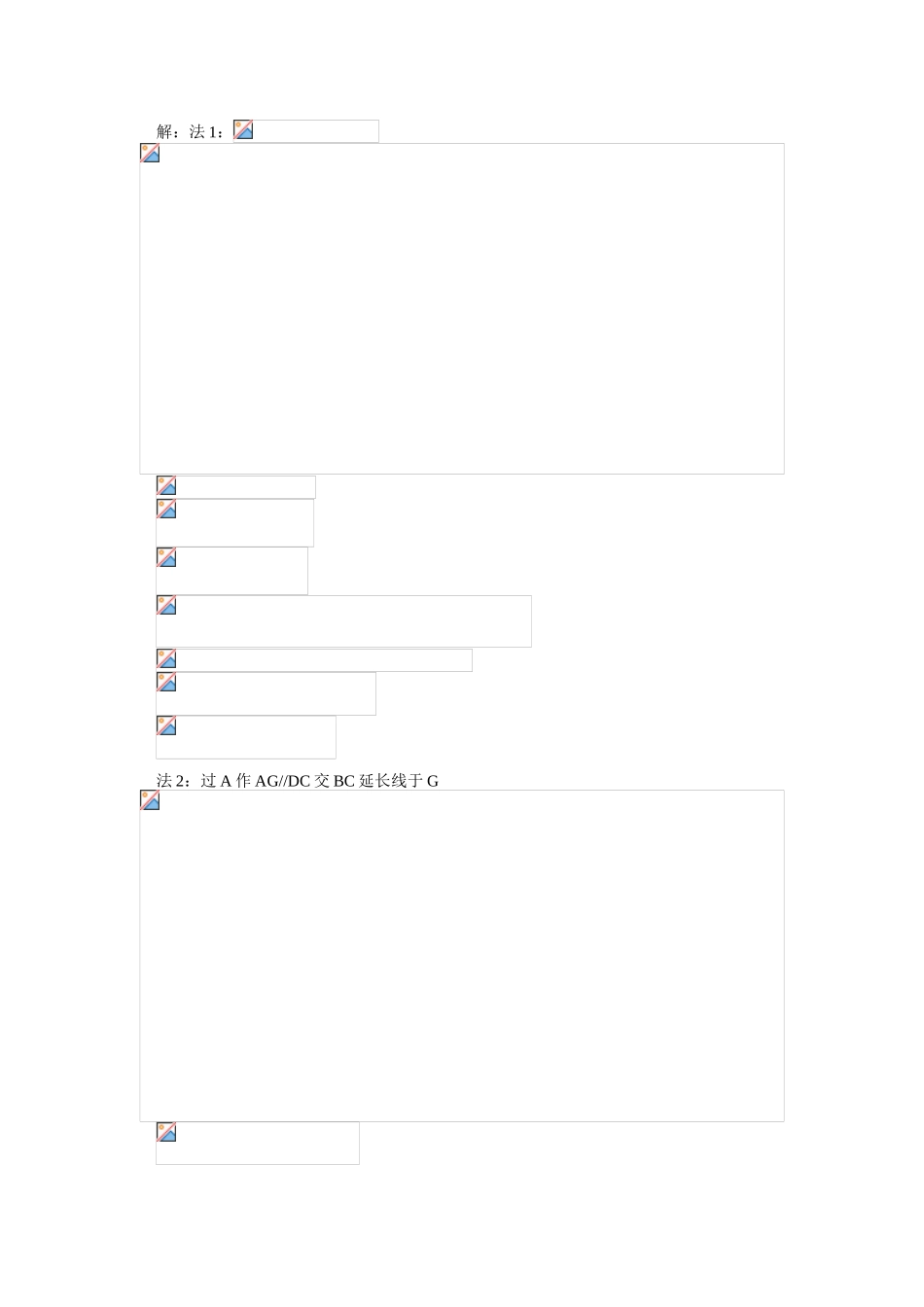
九年级数学解直角三角形人教版【同步教育信息】一.本周教学内容:解直角三角形学习目的:1.理解什么叫解直角三角形,并熟练掌握直角三角形的解法:依照题意画出符合条件的图形,写出正确的解题过程。2.会利用直角三角形解决一些斜三角形或四边形中的问题。3.进一步体会“转化的思想”,“方程的思想”在解直角三角形中的作用,提高分析问题,解决问题的能力。通过本周的学习,我们知道,解直角三角形就是只要知道直角三角形中除直角以外的五个元素中的2个(其中至少有一个是边),去求出其它未知元素的过程,一般地就是这么四种情况:(1)已知:a、b,解这个三角形。(2)已知:a、c,解这个三角形。(3)已知:a,∠A,解这个三角形。(4)已知:c,∠A,解这个三角形。我们只须运用(1)勾股定理,(2)直角三角形两锐角互余,(3)锐角三角函数就可以轻松求出未知元素。以下我们来看几道例题。【例题分析】例1.已知:在RtΔABC,∠C=90°,AD平分∠CAB,若CD:DB=1:2,AC=3,解这个直角三角形。解:请大家注意该题条件是“AD平分∠BAC”我们利用了“角平分线上的点到这个角两边的距离相等”这一重要性质,同学们也可试着过D点作AC的平行线来完成。例2.边上的高AE的长。解:法1:法2:过A作AG//DC交BC延长线于G这两种做法都利用平行线转移比例关系,同时构造了必要的直角三角形。例3.如图,已知:在ΔABC中,∠ABC=135°,P为AC上一点,且∠PBA=90°,CP:PA=1:2。(1)求tan∠APB。(2)若PB=2,求AC长。解:法1:法2:过P点作PD//AB交BC于D法3:过C点作CF//AB交BP延长线于F同学们可以自己完成这一辅助线作法的解答。可见,这三种做法的共同之处都是利用平行线转到了线段比CP:PA=1:2,同时,构造了等腰直角三角形,这当然是利用了已知条件中的∠ABC=135°。例4.解:的长。同学们可以动手做一做。例6.如图,∠A=∠C=90°,BC=CD,AC平分∠BAD,AB=7,AD=5,求AC及四边形ABCD的面积。解:法1:这种作法利用了角平分线的性质,与例1辅助线的作法类似。法2:在AB上截取AE=AD,连结CE这种方法是利用角平分线是这个角的对称轴,而构造全等三角形。法3:过点C作EC⊥CA交AD延长线于E这种方法可看作将ΔACB绕着C点旋转了90°,得到ΔECD,构造了全等三角形。【模拟试题】一.选择题(只有一个答案正确)1.在A.B.C.D.2.在中,A.B.C.D.3.等腰三角形底角的余弦值为,腰长为10,则腰上的高为()A.B.C.8D.4.在中,,则a、b、c的长分别为()A.4,5,B.3,4,5C.8,10,D.8,6,105.在A.B.C.D.36.在,则等于()A.B.C.D.7.等腰梯形中位线长10,面积,上底是5,则它的下底上的角的正切值为()A.B.C.D.二.填空题:1.如图,,若,则AC=_______,________,AD=__________。2.在中,,如果,则_________,_________。3.在4.如图,中,,D为AC上一点,且,则5.已知:6.在中,,则。三.解答题:1.如图,,求k及AB、AC、BC长。2.如图,钝角三角形ABC中,,于A,求及腰上的高。3.,求三条边的长及BC边上的高。4.,AD为BC上的高,且BD=1,求的面积。5.如图,中,于D,,求的面积。【试题答案】一.1.B2.A3.D4.D5.C6.D7.B二.1.2.3.4.5.70,746.三.1.2.3.4.5.