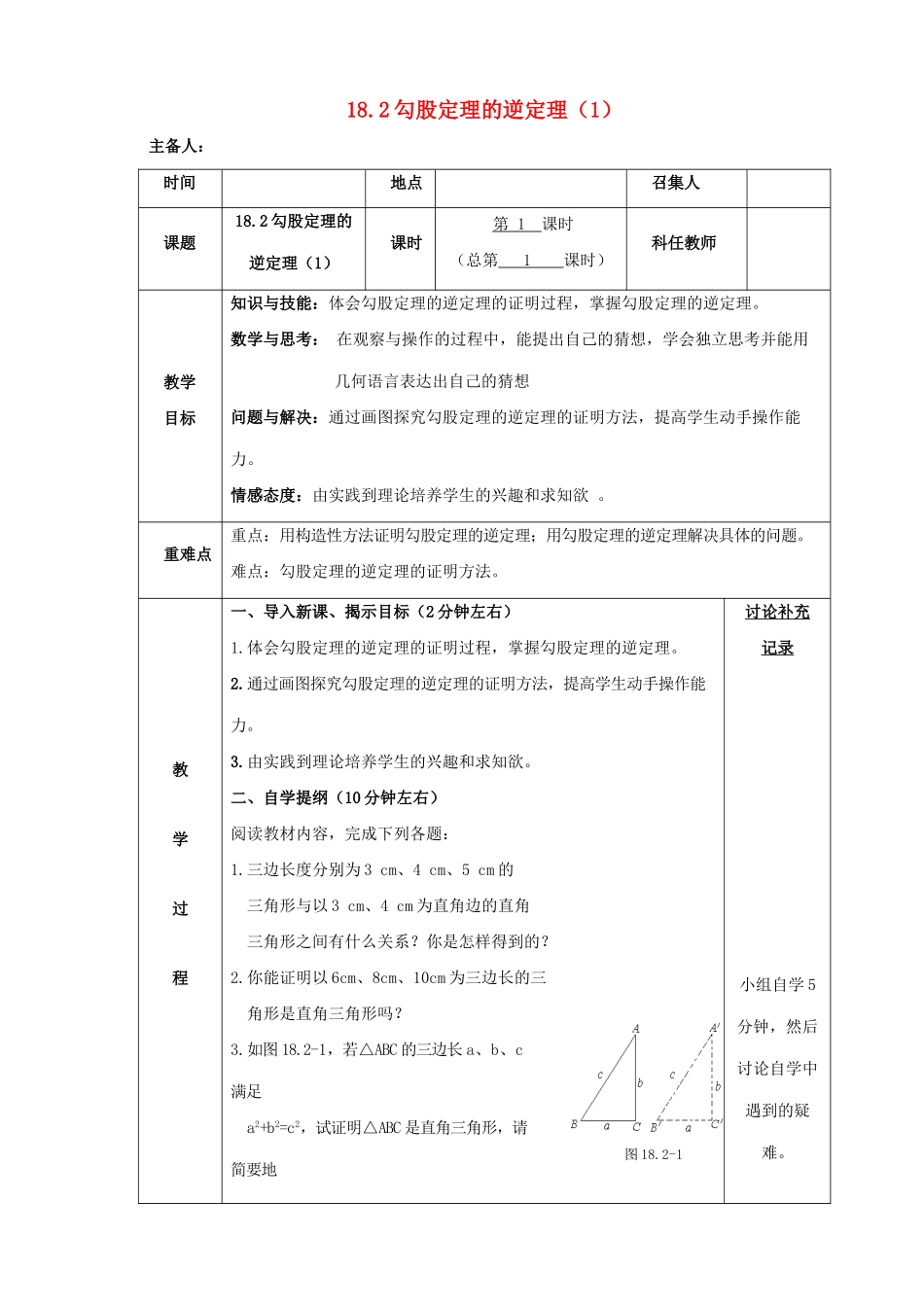
图18.2-118.2勾股定理的逆定理(1)主备人:时间地点召集人课题18.2勾股定理的逆定理(1)课时第1课时(总第1课时)科任教师教学目标知识与技能:体会勾股定理的逆定理的证明过程,掌握勾股定理的逆定理。数学与思考:在观察与操作的过程中,能提出自己的猜想,学会独立思考并能用几何语言表达出自己的猜想问题与解决:通过画图探究勾股定理的逆定理的证明方法,提高学生动手操作能力。情感态度:由实践到理论培养学生的兴趣和求知欲。重难点重点:用构造性方法证明勾股定理的逆定理;用勾股定理的逆定理解决具体的问题。难点:勾股定理的逆定理的证明方法。教学过程一、导入新课、揭示目标(2分钟左右)1.体会勾股定理的逆定理的证明过程,掌握勾股定理的逆定理。2.通过画图探究勾股定理的逆定理的证明方法,提高学生动手操作能力。3.由实践到理论培养学生的兴趣和求知欲。二、自学提纲(10分钟左右)阅读教材内容,完成下列各题:1.三边长度分别为3cm、4cm、5cm的三角形与以3cm、4cm为直角边的直角三角形之间有什么关系?你是怎样得到的?2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?3.如图18.2-1,若△ABC的三边长a、b、c满足a2+b2=c2,试证明△ABC是直角三角形,请简要地讨论补充记录小组自学5分钟,然后讨论自学中遇到的疑难。写出证明过程,由此你能得出什么结论?4.问题3中的结论与勾股定理之间有怎样的关系?5.例在△ABC中,a=15,b=17,c=8,求此三角形的面积。三、合作探究,解决疑难(12分钟左右)1.解决自学提纲中的问题。据说,几千年前的古埃及人就已经知道,在一根绳子上连续打上等距离的13个结,然后用钉子将第1个与第13个结钉在一起,拉紧绳子,再在第4个和第8个结处各钉上一个钉子,如图18.2-2。这样围成的三角形中,最长边所对的角就是直角。知道为什么吗?2.用圆规、直尺作△ABC,使AB=10cm,AC=6cm,BC=8cm和AB=13cm,BC=5cm,AC=12cm。量一量∠C,它是90°吗?再画一个△ABC,使它的三边长分别是6cm、8cm、10cm,这个三角形有什么特征?为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?(二)猜想:如果一个三角形的三边长a、b、c满足下面的关系a2+b2=c2,那么这个三角形是直角三角形吗?试着证明:已知:在△ABC中,AB=c,BC=a,AC=b,并且a2+b2=c2.求证:∠C=90°.勾股定理的逆定理如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.例1根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形。如果是,指出哪条边所对的角是直角?(1)a=7,b=24,c=25;(2)a=7,b=8,c=11.由问题1引导学生得出证明方法讨论补充记录图18.2-2解:(1) 最大边是c=25,c2=625,a2+b2=72+242=625,∴a2+b2=c2,∴△ABC是直角三角形,最大边c所对的角是直角.(2)该三角形不是直角三角形.四、巩固新知,当堂训练(10分钟)1.判断下列三个边长组成的三角形是不是直角三角形?(1)a=2,b=3,c=4.(2)a=9,b=7,c=12.(3)a=25,b=20,c=15.(4)a:b:c=3:4:5。五、课堂小结(3分钟)通过本节课的学习,你有哪些收获?六、课外作业,拓展延伸(8分钟)板书设计教学反思18.2勾股定理的逆定理(2)主备人:时间地点召集人课题18.2勾股定理的逆定理(2)课时第2课时(总第2课时)科任教师教学目标知识与技能:进一步掌握勾股定理的逆定理,并会应用勾股定理的逆定理判断一个三角形是否是直角三角形,能够理解勾股定理及其逆定理的区别与联系,掌握它们的应用范围。数学与思考:能在解题过程中发展数感,能对勾股数进行归类,形成独立的思维能力。问题解决:在自主、合作、探究过程中,解决相关问题,培养与他人合作的优良品质。情感态度:培养数学思维以及合情推理意识,感悟勾股定理和逆定理的应用价值。重难点重点:勾股定理的逆定理难点:勾股定理的逆定理的应用教一、导入新课、揭示目标(2分钟左右)1.进一步掌握勾股定理的逆定理,并会应用勾股定理的逆定理判断一个三角形是否是直角三角形,能够理解勾股定理及其逆定理的区别与联系,掌握它们的应用范围。2.培养逻辑推理能力,体会“形”与“...