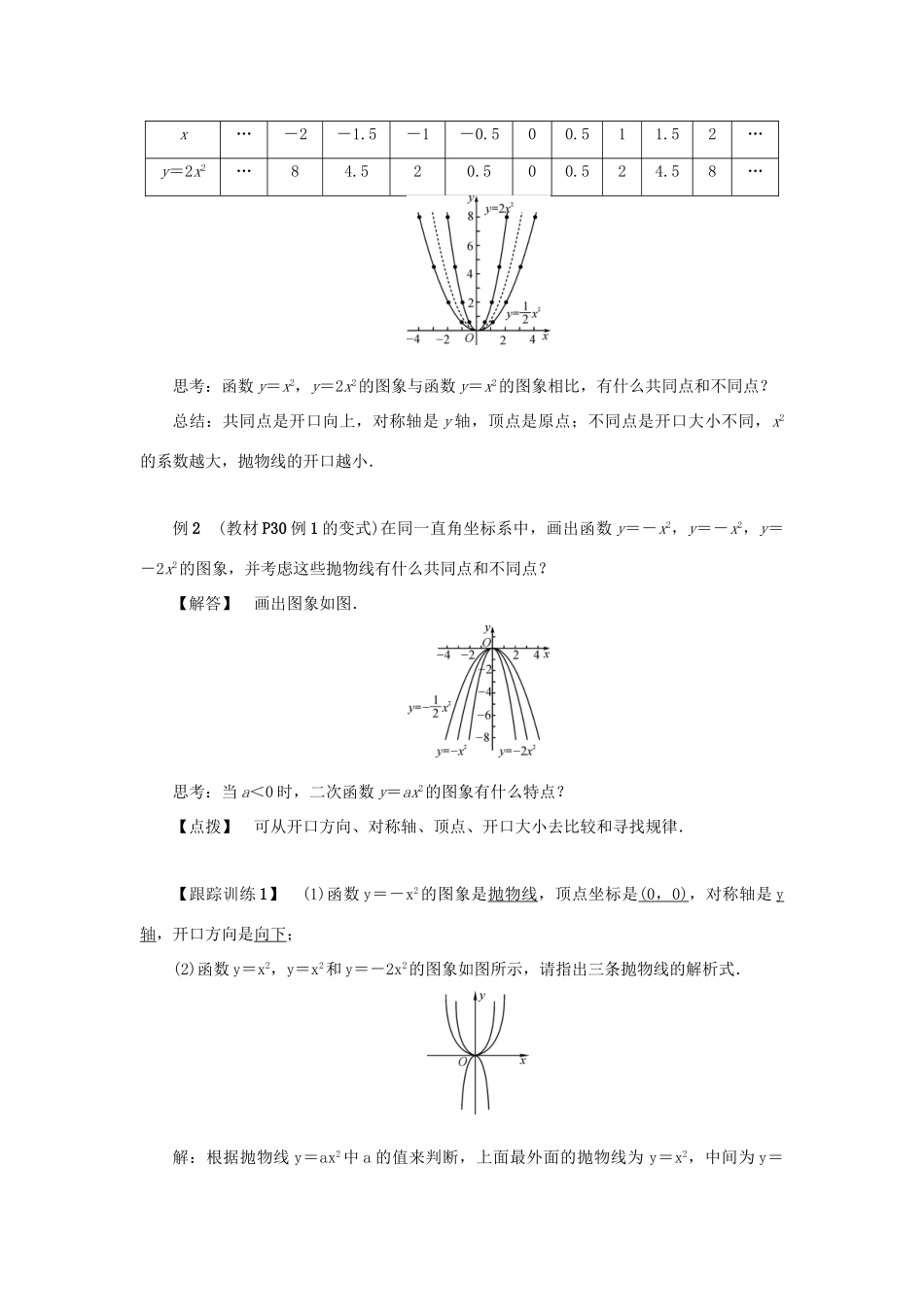
22.1.2二次函数y=ax2的图象和性质01教学目标1.能够用描点法画函数y=ax2的图象,并能根据图象认识和理解其性质.2.初步建立二次函数表达式与图象之间的联系,体会数与形的结合与转化.02预习反馈阅读教材P30~32,自学“例1”“思考”“探究”“归纳”,掌握用描点法画函数y=ax2图象的方法,理解其性质,完成下列内容.1.一般地,当a>0时,抛物线y=ax2的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.2.一般地,当a<0时,抛物线y=ax2的开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.3.从二次函数y=ax2的图象可以看出:如果a>0,当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;如果a<0,当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.4.(1)抛物线y=2x2的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点;(2)抛物线y=-3x2的开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点;(3)在抛物线y=2x2对称轴的左侧,y随x的增大而减小,在对称轴的右侧,y随x的增大而增大;(4)在抛物线y=-3x2对称轴的左侧,y随x的增大而增大,在对称轴的右侧,y随x的增大而减小.03新课导入回顾:一次函数的图象是一条直线.思考:二次函数的图象是什么形状呢?还记得如何用描点法画一个函数的图象吗?画函数图象的一般步骤:列表、描点、连线.导入:你能画出二次函数y=x2的图象吗?第一步:列表:x…-3-2-10123…y=x2…9410149…第二步:描点,在平面直角坐标系中描出表中各点,如图1.图1图2第三步:连线,用平滑的曲线顺次连接各点,就得到二次函数y=x2的图象,如图2.思考:观察函数y=x2的图象,它有什么特点?总结:(1)二次函数的图象是一条曲线,它的开口向上,这条曲线叫做抛物线;(2)抛物线y=x2的对称轴是y轴,抛物线与它的对称轴的交点是(0,0),它是图象的最低点,叫做抛物线的顶点;(3)在对称轴的左侧,抛物线y=x2从左到右下降;在对称轴的右侧,抛物线y=x2从左到右上升.也就是说,当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.04新课讲授例1(教材P30例1)在同一直角坐标系中,画出函数y=x2,y=2x2的图象.【解答】分别列表,画出它们的图象,如图.x…-4-3-2-101234…y=x2…84.520.500.524.58…x…-2-1.5-1-0.500.511.52…y=2x2…84.520.500.524.58…思考:函数y=x2,y=2x2的图象与函数y=x2的图象相比,有什么共同点和不同点?总结:共同点是开口向上,对称轴是y轴,顶点是原点;不同点是开口大小不同,x2的系数越大,抛物线的开口越小.例2(教材P30例1的变式)在同一直角坐标系中,画出函数y=-x2,y=-x2,y=-2x2的图象,并考虑这些抛物线有什么共同点和不同点?【解答】画出图象如图.思考:当a<0时,二次函数y=ax2的图象有什么特点?【点拨】可从开口方向、对称轴、顶点、开口大小去比较和寻找规律.【跟踪训练1】(1)函数y=-x2的图象是抛物线,顶点坐标是(0,0),对称轴是y轴,开口方向是向下;(2)函数y=x2,y=x2和y=-2x2的图象如图所示,请指出三条抛物线的解析式.解:根据抛物线y=ax2中a的值来判断,上面最外面的抛物线为y=x2,中间为y=x2,在x轴下方的为y=-2x2.【点拨】抛物线y=ax2,当a>0时,开口向上;当a<0时,开口向下,|a|越大,开口越小.例3(补充例题)已知函数y=(m+2)xm2+m-4是关于x的二次函数.(1)求满足条件的m的值;(2)当m为何值时,抛物线有最低点?求这个最低点;(3)当x为何值时,y随x的增大而增大?当x为何值时,y随x的增大而减小?【解答】(1)由题意,得解得∴当m=2或m=-3时,函数为二次函数.(2)若抛物线有最低点,则抛物线开口向上,∴m+2>0,即m>-2.∴m=2.这个最低点为抛物线的顶点,其坐标为(0,0),(3)当x>0时,y随x的增大而增大;当x>0时,y随x的增大而减小.【点拨】也可结合图象来分析完成此题.【跟踪训练2】已知函数y=(m-1)xm2-2m+2+(m-2)x是二次函数,且开口向上.求m的值及二次函数的解析式,并回答y随x的变化规律.解:由题意有解得m=0(舍去),m...