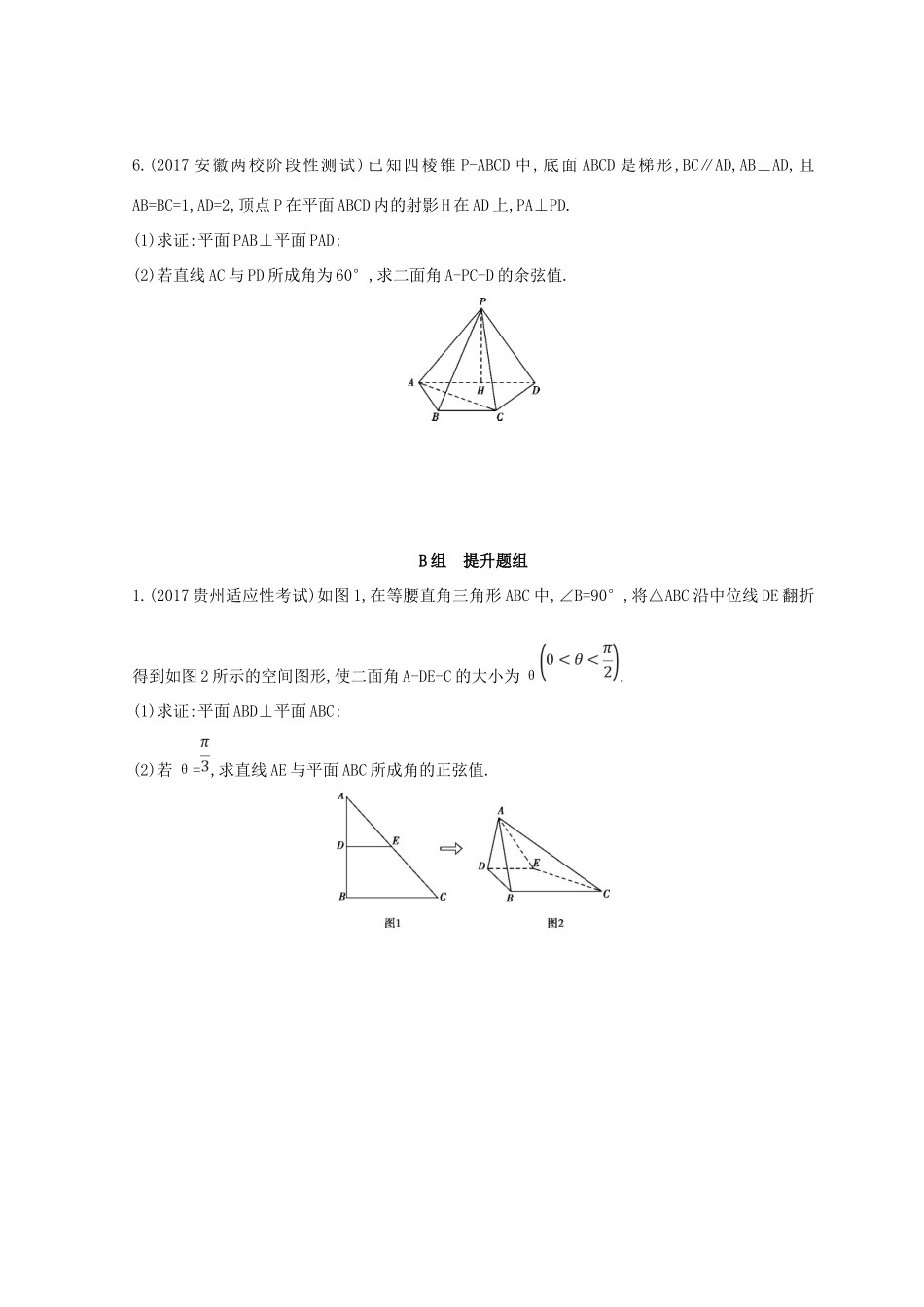
第3讲空间向量与立体几何A组基础题组1.(2017云南第一次统一检测)如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=1,BB1=1,P是AB的中点,则异面直线BC1与PD所成的角等于()A.30°B.45°C.60°D.90°2.(2017云南第一次统一检测)已知三棱锥P-ABC的所有顶点都在表面积为16π的球O的球面上,AC为球O的直径.当三棱锥P-ABC的体积最大时,二面角P-AB-C的大小为θ,则sinθ=()A.B.C.D.3.正方体ABCD-A1B1C1D1的棱长为1,若动点P在线段BD1上运动,则·的取值范围是.4.在正三棱柱ABC-A1B1C1中,AB=4,点D在棱BB1上,若BD=3,则AD与平面AA1C1C所成角的正切值为.5.(2017课标全国Ⅰ,18,12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.6.(2017安徽两校阶段性测试)已知四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2,顶点P在平面ABCD内的射影H在AD上,PA⊥PD.(1)求证:平面PAB⊥平面PAD;(2)若直线AC与PD所成角为60°,求二面角A-PC-D的余弦值.B组提升题组1.(2017贵州适应性考试)如图1,在等腰直角三角形ABC中,∠B=90°,将△ABC沿中位线DE翻折得到如图2所示的空间图形,使二面角A-DE-C的大小为θ.(1)求证:平面ABD⊥平面ABC;(2)若θ=,求直线AE与平面ABC所成角的正弦值.2.如图,正方形ADEF所在的平面和等腰梯形ABCD所在的平面互相垂直,已知BC=4,AB=AD=2.(1)求证:AC⊥BF;(2)在线段BE上是否存在一点P,使得平面PAC⊥平面BCEF?若存在,求出的值;若不存在,请说明理由.答案精解精析A组基础题组1.C如图,取A1B1的中点E,连接D1E,AD1,AE,则∠AD1E即为异面直线BC1与PD所成的角.因为AB=2,所以A1E=1,又BC=BB1=1,所以D1E=AD1=AE=,所以△AD1E为正三角形,所以∠AD1E=60°,故选C.2.C设球O的半径为R,由4πR2=16π,得R=2,设点P到平面ABC的距离为d,则0
==-.易知二面角A-PB-C为钝二面角,所以二面角A-PB-C的余弦值为-.6.解析(1)证明: PH⊥平面ABCD,AB⊂平面ABCD,∴PH⊥AB. AB⊥AD,AD∩PH=H,AD,PH⊂平面PAD,∴AB⊥平面PAD.又AB⊂平面PAB,∴平面PAB⊥平面PAD.(2)以A为原点,建立空间直角坐标系A-xyz,如图, PH⊥平面ABCD,∴z轴∥PH.则A(0,0,0),C(1,1,0),D(0,2,0),设AH=a,PH=h(00),则P(0,a,h),∴=(0,a,h),=(0,a-2,h),=(1,1,0). PA⊥PD,∴·=a(a-2)+h2=0.① AC与PD所成的角为60°,∴|cos<,>|==,∴(a-2)2=h2,②由①②得(a-2)(a-1)=0, 00,∴h=1,∴P(0,1,1).∴=(0,1,1),=(1,1,0),=(1,0,-1),=(1,-1,0),设平面APC的法向量为n=(x1,y1,z1),由得平面APC的一个法向量为n=(1,-1,1),设平面DPC的法向量为m=(x2,y2,z2).由得平面DPC的一个法向量为m=(1,1,1).∴cos==. 二面角A-PC-D的平面角为钝角,∴二面角A-PC-D的余弦值为-.B组提升题组1.解析(1)证明:在等腰直角三角形ABC中,AB⊥BC,且DE为△ABC的中位线,∴DE∥BC,∴DE⊥AB.由翻折,可知DE⊥AD,DE⊥DB,AD∩DB=...