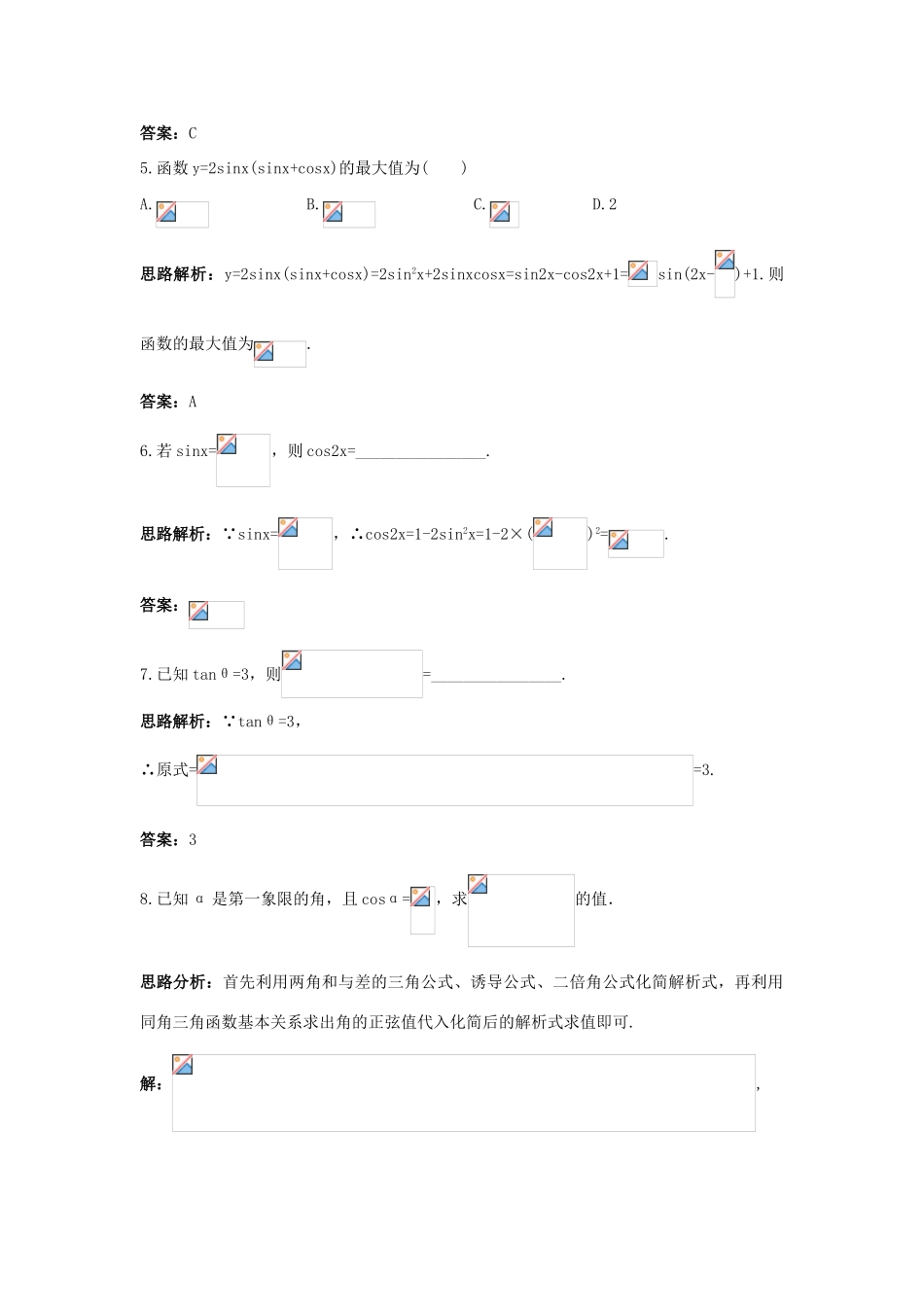
高中数学第3章三角恒等变换3.2二倍角的三角函数达标训练苏教版必修4基础·巩固1.sin215°+cos215°+cos75°sin75°的值等于()A.B.C.D.思路解析:原式=sin215°+cos215°+sin15°cos15°=1+sin30°=1+=.答案:C2.cos4-sin4的值等于()A.0B.C.1D.思路解析:原式=(cos2+sin2)(cos2-sin2)=cos=0.答案:A3.(cos-sin)(cos+sin)等于()A.-B.-C.D.思路解析:(cos-sin)(cos+sin)=cos2-sin2=cos=,故选择C.答案:C4.已知sin2α=,α∈(,),则cosα+sinα的值是()A.-B.C.D.-思路解析:∵α∈(,),∴sinα>0,cosα>0.又∵(cosα+sinα)2=1+sin2α=1+=,∴cosα+sinα=.答案:C5.函数y=2sinx(sinx+cosx)的最大值为()A.B.C.D.2思路解析:y=2sinx(sinx+cosx)=2sin2x+2sinxcosx=sin2x-cos2x+1=sin(2x-)+1.则函数的最大值为.答案:A6.若sinx=,则cos2x=________________.思路解析:∵sinx=,∴cos2x=1-2sin2x=1-2×()2=.答案:7.已知tanθ=3,则=________________.思路解析:∵tanθ=3,∴原式==3.答案:38.已知α是第一象限的角,且cosα=,求的值.思路分析:首先利用两角和与差的三角公式、诱导公式、二倍角公式化简解析式,再利用同角三角函数基本关系求出角的正弦值代入化简后的解析式求值即可.解:,由已知可得sinα=,∴原式=×.综合·应用9.的值是()A.1B.2C.4D.思路解析:原式===2.答案:B10.化简+为()A.B.C.D.思路解析:由于,则原式==.答案:C11.已知-2cos(α+β)=2,则sin2β+2cos2α的值为________________.思路解析:由于-2cos(α+β)=-cos(α+β)==2,所以sin2β=4sin2α.所以sin2β+2cos2α=sin2β+2-4sin2α=2.答案:212.已知=2006,则+tan2α的值是______________.思路解析:由=2006,可得tanα=.又+tan2α=sin2α+-sin2α+=+==2006.答案:200613.已知函数f(x)=sin2x+2sinxcosx+3cos2x,x∈R,求:(1)函数f(x)的最大值及取得最大值的自变量x的集合;(2)函数f(x)的单调增区间.思路分析:本小题利用三角公式将函数解析式化为y=Asin(ωx+φ)+B(A>0,ω>0)的形式再求解.(1)解法一:∵f(x)=+sin2x+2+sin2x+cos2x=2+sin(2x+).∴当2x+=2kπ+,即x=kπ+(k∈Z)时,f(x)取得最大值2+,因此,f(x)取得最大值的自变量x的集合是{x|x=kπ+,k∈Z}.解法二:∵f(x)=(sin2x+cos2x)+sin2x+2cos2x=1+sin2x+1+cos2x=2+sin(2x+),∴当2x+=2kπ+,即x=kπ+(k∈Z)时,f(x)取得最大值2+.因此,f(x)取得最大值的自变量x的集合是{x|x=kπ+,k∈Z}.(2)解:f(x)=2+sin(2x+).由题意得2kπ-≤2x+≤2kπ+(k∈Z),即kπ-≤x≤kπ+(k∈Z).因此,f(x)的单调增区间是[kπ-,kπ+](k∈Z).回顾·展望14.(2006辽宁高考)已知等腰△ABC的腰为底的2倍,则顶角A的正切值是()A.B.C.D.思路解析:利用等腰三角形中的边关系求出顶角半角正切,再利用二倍角公式求解.答案:D15.(2006江西高考)已知tan=3,则cosα等于()A.B.-C.D.-思路解析:cosα==-.答案:B16.(2006淅江高考)函数y=2sinxcosx-1,x∈R的值域是________________.思路解析:利用二倍角公式将解析式化为y=sin2x-1,再利用正弦函数的性质求解即可.答案:[-2,0]17.(2006淅江高考)函数y=sin2x+sin2x,x∈R的值域是()A.[-,]B.[-,]C.[-+,+]D.[--,-]思路解析:综合利用两角和与差的三角公式、二倍角公式将函数解析式化为y=Asin(ωx+φ)+B(A>0,ω>0),然后再利用它的性质求解.答案:C18.(2006安徽高考)已知0<α<,sinα=.(1)求的值;(2)求tan(α-)的值.思路分析:本题主要利用同角三角函数基本关系、两角和与差的三角公式、倍角公式等基础知识.利用同角三角函数基本关系式和角的范围求出角的余弦值即可求解.解:(1)由0<α<,sinα=,得cosα=,所以==20.(2)∵tanα==,∴tan(α-)==.19.(2006北京高考)已知函数f(x)=.(1)求f(x)的定义域;(2)设α是第四象限的角,且tanα=-,求f(α)的值.思路分析:本题主要利用三角函数的性质、同角三角函数基本关系式、倍角公式等基础知识.由正切值及角的范围可求出角的正、余弦值.解:(1)由cosx≠0得x≠kπ+(k∈Z),故f(x)的定义域为{x|x≠kπ+,k∈Z}.(2)∵α是第四象限角,tanα=-,则cosα=,sinα=-=-.故f(α)=.20.求函数y=2cos(x+)cos(x-)+sin2x的值域和最小正周期.思路分析:利用两角和与差的三角公式将函数的解析式化为y=Asin(ωx+φ)+B(A>0,ω>0)的形式,再利用它的性质求解.解:y=2cos(x+)cos(x-)+sin2x=2(cosx-sinx)(cosx+sinx)+sin2x=cos2x-sin2x+sin2x=cos2x+sin2x=2(cos2x+sin2x)=2sin(2x+).∴函数的值域为[-2,2],最小正周期为π.