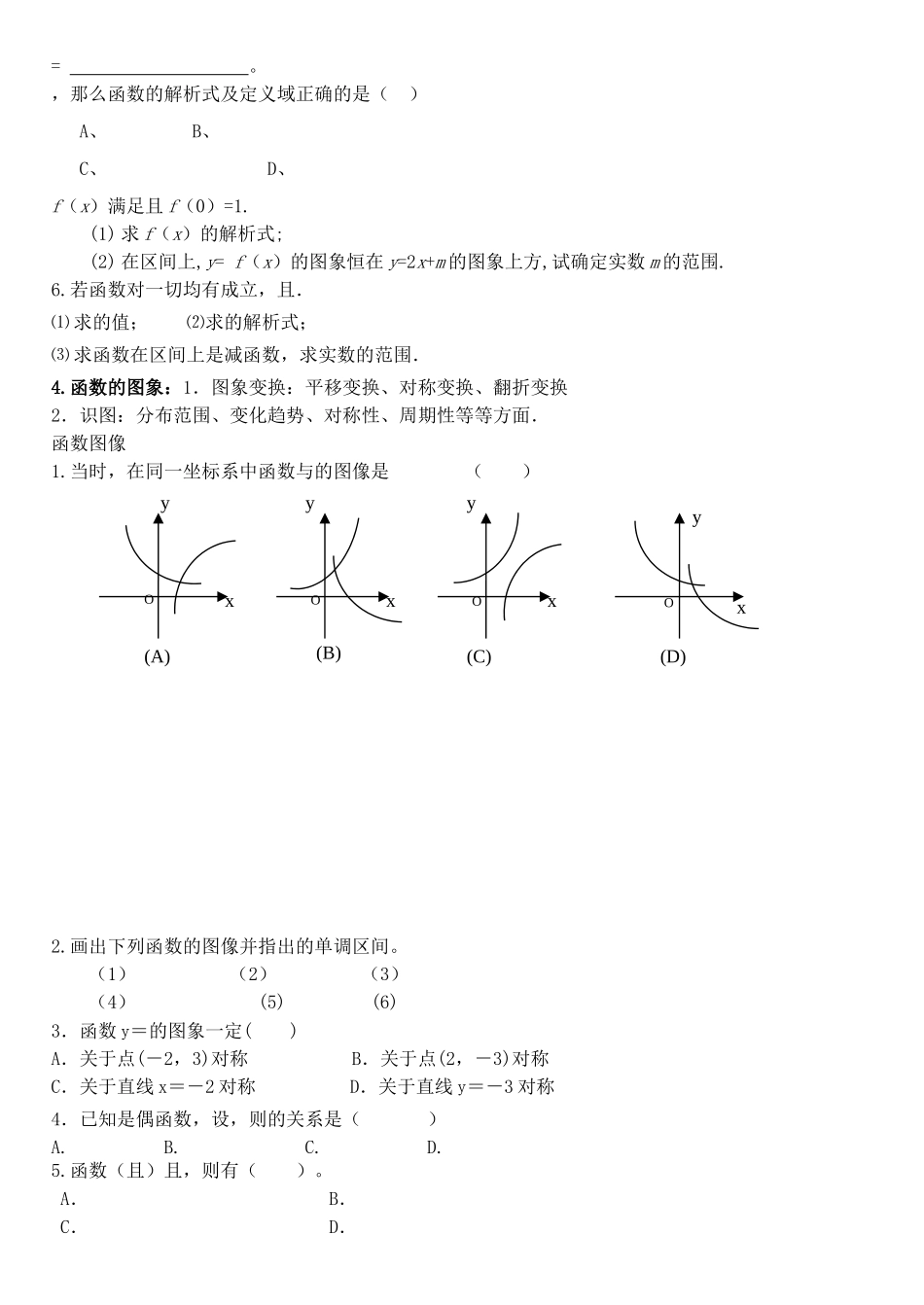
集合的概念1、下列各式:①;②;③;④,其中错误的个数是()A.1个B.2个C.3个D.4个2.已知集合,,,,,则()3.若集合,,且,则4.已知,,若,则适合条件的实数的集合为;的子集有个;的非空真子集有个.5.集合A={一条边长为2,一个角为30°的等腰三角形},则集合A中的元素的个数为()A.2B.3C.4D.无数个6.设集合,,则()7.满足条件{1,2,3}M{1,2,3,4,5,6}的集合M的个数是()A.8B.7C.6D.58.设全集,若,,,则,.9.调查100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么既带感冒药又带胃药的人数的最大值为,最小值为.10.已知全集,集合,,则集合是11.已知:,,则实数、的值分别为.12.若集合,集合,且,求实数的取值范围.13.设集合,,若,则的取值范围是(A)(B)(C)(D)()是两个集合,定义,若,则()<≤,,A和B都是U的子集,且有:∩,(CUA)∩B={7,8},CU,求集合A和B。16.已知全集U=R,A={x|x-1|≥1},B={x|≥0},求:A∩B;(2)17.已知集合,,(1)若求a的取值范围.(2)若,求a的取值范围.18.已知集合,若,求实数的取值范围.19.已知集合,(1)若中有两个元素,求实数的取值范围;(2)若中至多有一个元素,求实数的取值范围.映射与函数概念及单调性、奇偶性小结1.基本概念:函数和映射(任意对唯一),相同函数,象与原象1.已知集合A=,B=,下列从A到B的对应不是映射的是(A)(B)(C)(D)2.已知集合A=,B=,下列从A到B的对应不是映射的是(A)(B)(C)(D)表示同一个函数的是(A)(B)(C)(D)4.设是从集合A到B的映射,,,若B中元素(6,2)在映射下的原象是(3,1),则的值分别为________.,则使得的自变量的取值范围是___。2。求函数定义域的主要依据:(抽象函数记住定义域指x的范围,桥梁是括号内整体范围一样)(1)分式分母不为零;(2)偶数次方根的被开方数不小于零;(3)零次幂的底数不能为零。(4)由多个函数组合应该取他们的交集(5)分段函数应每一段的定义域合起来。(6)复合函数特别注意内层函数的值域与外层函数定义域的关系。(7)实际问题定义域必须有实际意义(特别是应用题时写函数解析式时注意隐含范围),(8)对含参数的函数定义域要对字母参数分类讨论。的定义域为()A.(-1,0)B.-1,0C.[-1,0]D.[-1,4]2.函数的定义域为3.若函数的定义域为R,则4.已知f()的定义域为[1,2],则y=f(的定义域为_______.3.求函数值域与最值的常用方法:(注意方法的归类,等号是否能取到)(1)观察法;简单函数及一次分式函数(直接推算时,一定注意定义域)(2)配方法:适用于二次函数或可化为二次函数的函数,(注意对称轴与区间的位置)(3)判别式法:主要适用于的二次方程分式函数(注意分子分母无公因式可约)(4)换元法:带根式的函数(用换元法时一定要注意新变元的取值范围)(5)数形结合法:图形较容易画出借助图象直观求出(特殊函数:耐克及绝对值函数)(6)利用函数的单调性:要注意函数的单调性对函数最值的影响(前提是单调性已知)(7)反函数法(函数有界性法)(已知某些元素的范围时)的值域为()A、B、C、D、值域(1);(2);(3);(4)(5).(6)3.(1)函数的值域为.4.函数在上的值域是__________的值域是()A.[0,1]B.[-1,1]C.(-2,2)D.[-2,+]6.已知函数的值域为,求实数的值.7.设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+1=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域及值域.在区间[0,1]上有最小值-2,求的值.4.求函数解析式的常用方法:(1)待定系数法(已知函数的类型)、(2)配凑法(整体代换)、(3)换元法(复合函数)(4)消去法(互为倒数或相反数)(5)已知函数图像,求函数解析式;函数的解析式1.已知函数为一次函数,且是增函数,若,则。2.已知,则。是奇函数,是偶函数,且,则=。=。,那么函数的解析式及定义域正确的是()A、B、C、D、f(x)满足且f(0)=1.(1)求f(x)的解析式;(2)在区间上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.6.若函数对一切均有成立,且.⑴求的值;⑵求的解析式;...