高中数学 立体几何—空间点线面复习教案 苏教版必修2VIP免费

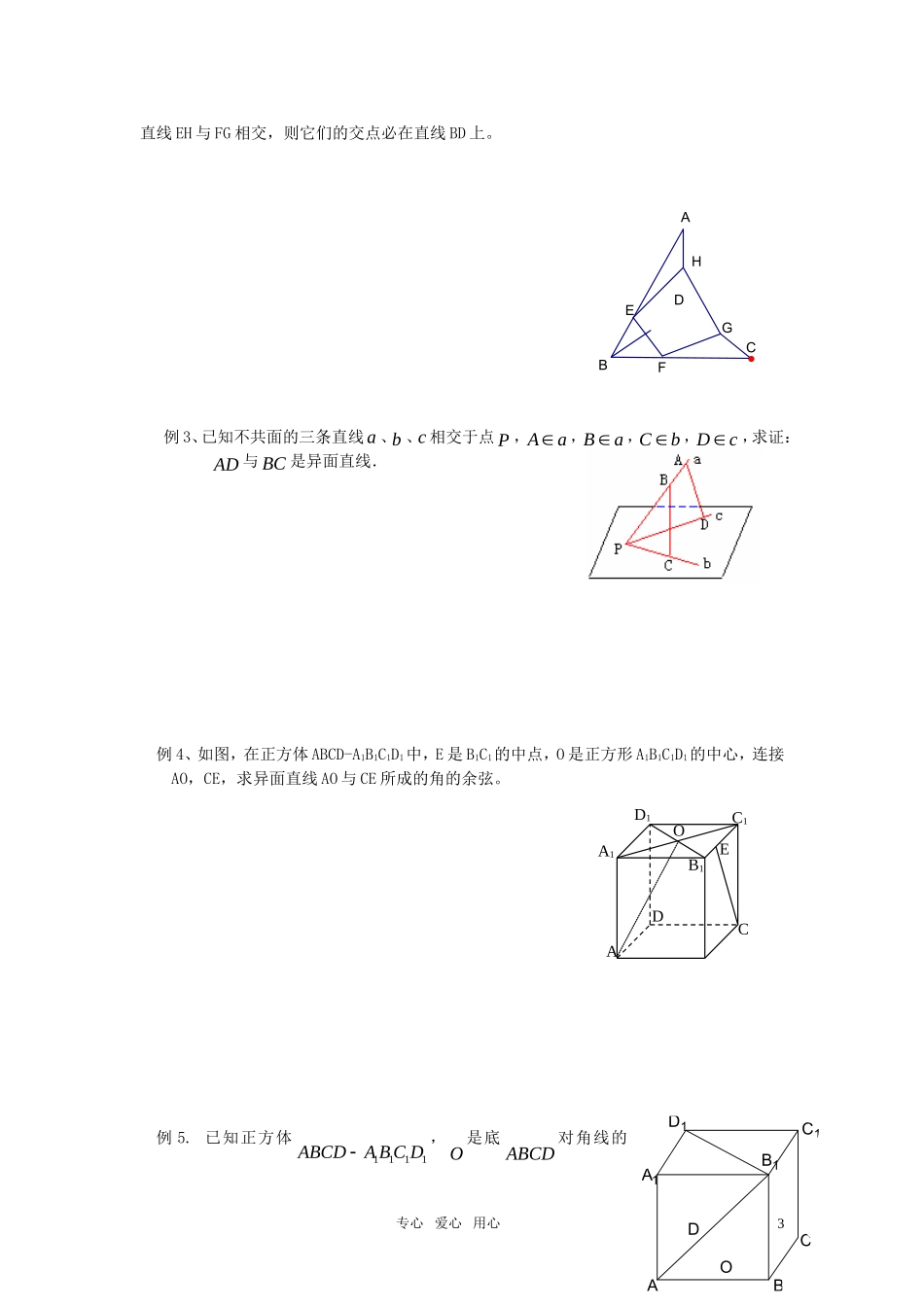
立体几何复习1．平面概述（1）平面的两个特征：①无限延展②平的（没有厚度）（2）平面的画法：通常画平行四边形来表示平面（3）平面的表示：用一个小写的希腊字母、、等表示，如平面、平面；用表示平行四边形的两个相对顶点的字母表示，如平面AC。2．三公理三推论:公理1：若一条直线上有两个点在一个平面内，则该直线上所有的点都在这个平面内：Al,Bl,A,Bl公理2：如果两个平面有一个公共点，那么它们还有其他公共点，且所有这些公共点的集合是一条过这个公共点的直线。公理3：经过不在同一直线上的三点，有且只有一个平面。推论一：经过一条直线和这条直线外的一点,有且只有一个平面。推论二：经过两条相交直线,有且只有一个平面。推论三：经过两条平行直线,有且只有一个平面。3．空间直线:（1）空间两条直线的位置关系：相交直线——有且仅有一个公共点；平行直线——在同一平面内，没有公共点；异面直线——不同在任何一个平面内，没有公共点。相交直线和平行直线也称为共面直线。异面直线的画法常用的有下列三种：（2）平行直线：公理4：平行于同一条直线的两条直线互相平行。（3）异面直线定理：连结平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线。推理模式：,,,ABaBaAB与a是异面直线。4．直线和平面的位置关系（1）直线在平面内（无数个公共点）；（2）直线和平面相交（有且只有一个公共点）；（3）直线和平面平行（没有公共点）——用两分法进行两次分类。它们的图形分别可表示为如下，符号分别可表示为a，aA，//a。专心爱心用心1abababaaAa5.线面平行①判定定理：如果不在一个平面内的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。推理模式：,,////ababa．②性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。推理模式：//,,//aabab．6．线线垂直判断线线垂直的方法：所成的角是直角，两直线垂直；垂直于平行线中的一条，必垂直于另一条。7．线面垂直定义：如果一条直线l和一个平面α相交，并且和平面α内的任意一条直线都垂直，我们就说直线l和平面α互相垂直奎屯王新敞新疆其中直线l叫做平面的垂线，平面α叫做直线l的垂面,直线与平面的交点叫做垂足。直线l与平面α垂直记作：l⊥α。直线与平面垂直的判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。●范题精讲：例1、已知：四边形ABCD中，AB‖DC，AB、BC、DC、AD分别与平面相交于点E、F、G、H。求证：点E、F、G、H在同一条直线上。例2、已知平面四边形EFGH的四个顶点分别在空间四边形ABCD的四条边上，求证：专心爱心用心2babaPPαDCBAEFHG直线EH与FG相交，则它们的交点必在直线BD上。例3、已知不共面的三条直线a、b、c相交于点P，aA，aB，bC，cD，求证：AD与BC是异面直线．例4、如图，在正方体ABCD-A1B1C1D1中，E是B1C1的中点，O是正方形A1B1C1D1的中心，连接AO，CE，求异面直线AO与CE所成的角的余弦。例5.已知正方体1111ABCDABCD，O是底ABCD对角线的专心爱心用心3ACDC1D1A1B1EOBAGFEHDCD1ODBAC1B1A1C交点.求证：（１）C1O∥面11ABD；（2）1AC面11ABD．例6如图，正三棱柱ABC--111CBA中（地面是正三角形，侧棱垂直于地面），D是BC的中点，AB=a.（1）求证：111CBDA（2）判断A1B与平面ADC1的位置关系，并证明你的结论例7如图，在多面体ABCDE中，AE面ABC，BD∥AE，且BDBCABAC2，1AE，F为CD中点．（1）求证：EF//平面ABC；（2）求证：EF平面BCD专心爱心用心4ABCC1B1A1DABCEDF图甲ADBCP图乙ADBCPEF例8如图,PA矩形ABCD所在平面,,MN分别是AB和PC的中点．(1)求证://MN平面;PAD(2)求证:;MNCD(3)若45PDA,求证:MN平面.PCD例9如图甲，在直角梯形PBCD中，PB∥CD，CD⊥BC，BC＝PB＝2CD，A是PB的中点.现沿AD把平面PAD折起，使得PA⊥AB（如图乙所示），E、F分别为BC、AB边的中点.（1）求证：PA⊥平面ABCD；（2）在PA上找一点G，使得FG∥平面PDE.专心爱心用心5ABCDMNP