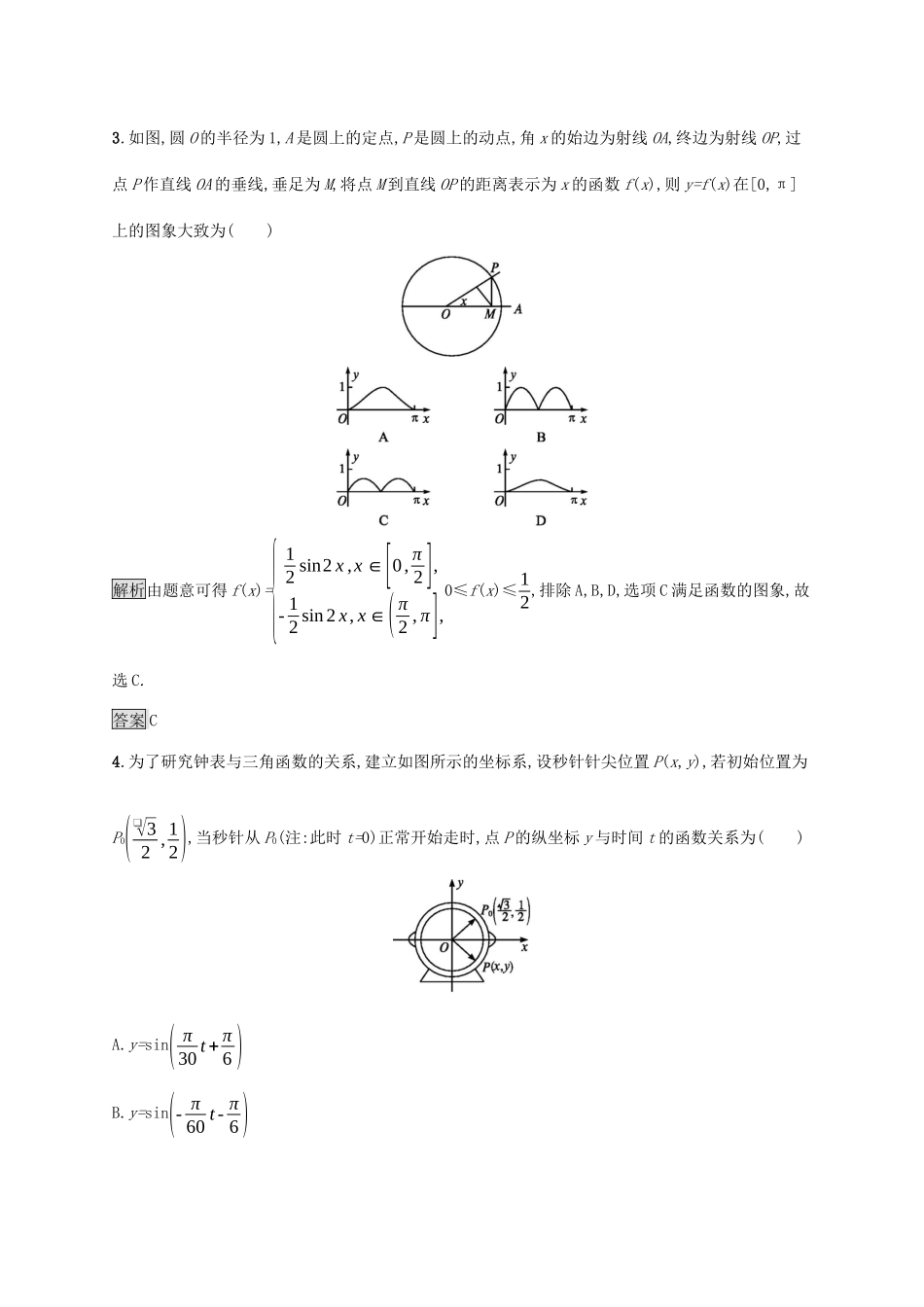
5.7三角函数的应用课后篇巩固提升1.如图,单摆从某点开始来回摆动,离开平衡位置O的距离s(单位:cm)和时间t(单位:s)的函数关系式为s=6sin(2πt+π6),那么单摆来回摆动一次所需的时间为()A.2πsB.πsC.0.5sD.1s解析单摆来回摆动一次所需的时间即为函数s=6sin(2πt+π6)的一个周期T=2π2π=1(s).答案D2.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是(12,❑√32),则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是()A.[0,1]B.[1,7]C.[7,12]D.[0,1]和[7,12]解析由已知可得该函数的周期为T=12,ω=2πT=π6.又当t=0时,A(12,❑√32),则y=sin(π6t+π3),由t∈[0,12],可解得函数的单调递增区间是[0,1]和[7,12].答案D3.如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]上的图象大致为()解析由题意可得f(x)={12sin2x,x∈[0,π2],-12sin2x,x∈(π2,π],0≤f(x)≤12,排除A,B,D,选项C满足函数的图象,故选C.答案C4.为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针针尖位置P(x,y),若初始位置为P0(❑√32,12),当秒针从P0(注:此时t=0)正常开始走时,点P的纵坐标y与时间t的函数关系为()A.y=sin(π30t+π6)B.y=sin(-π60t-π6)C.y=sin(-π30t+π6)D.y=sin(-π30t-π3)解析设y=sin(ωt+φ),其中ω<0.由2π|ω|=60,得|ω|=π30,∴ω=-π30.∴y=sin(-π30t+φ).又当t=0时,y=12,∴φ=π6.∴y=sin(-π30t+π6).答案C5.某地一天0~24时的气温y(单位:℃)与时间t(单位:h)的关系满足函数y=6sin(π12t-2π3)+20(t∈[0,24]),则这一天的最低气温是℃.解析因为0≤t≤24,所以-2π3≤π12t-2π3≤4π3,故当π12t-2π3=-π2,即t=2时函数取最小值-6+20=14.答案146.生物节律是描述体温、血压和其他易变的生理变化的每日生物模型.下表中给出了在24小时期间人的体温的典型变化(从夜间零点开始计时).时间(时)024681012温度(℃)36.836.736.636.736.83737.2时间(时)141618202224温度(℃)37.337.437.337.23736.8(1)作出这些数据的散点图;(2)选用一个三角函数来近似描述这些数据;(3)作出(2)中所选函数的图象.解(1)散点图如下:(2)设t时的体温y=Asin(ωt+φ)+C,则C=37.4+36.62=37,A=37.4-37=0.4,ω=2πT=2π24=π12.由0.4sin(π12×16+φ)+37=37.4,得sin(4π3+φ)=1,取φ=-5π6.故可用函数y=0.4sin(π12t-5π6)+37来近似描述这些数据.(3)图象如下: