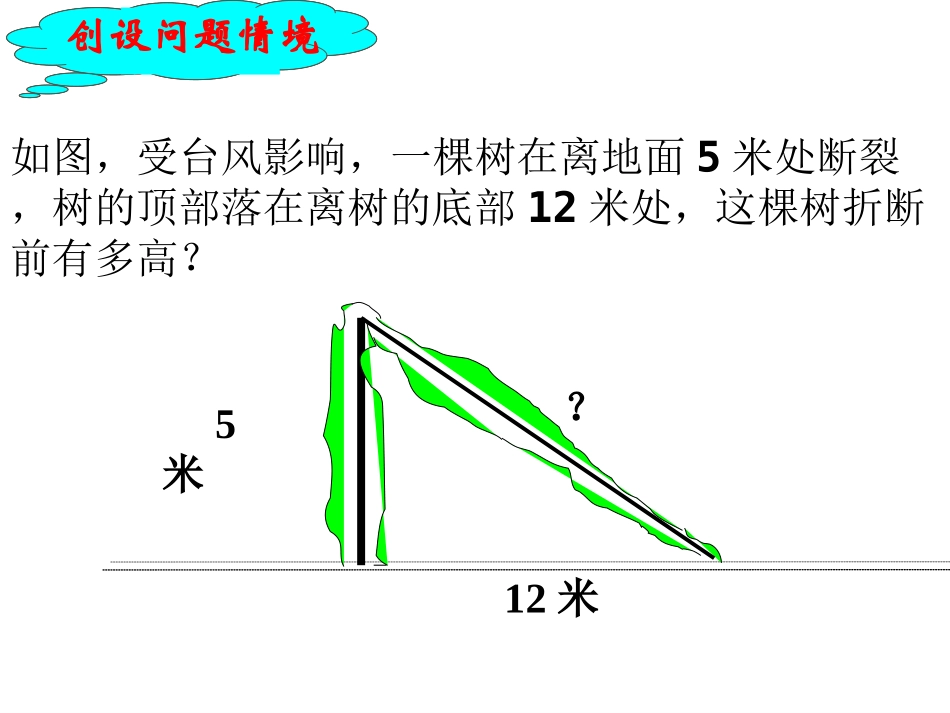
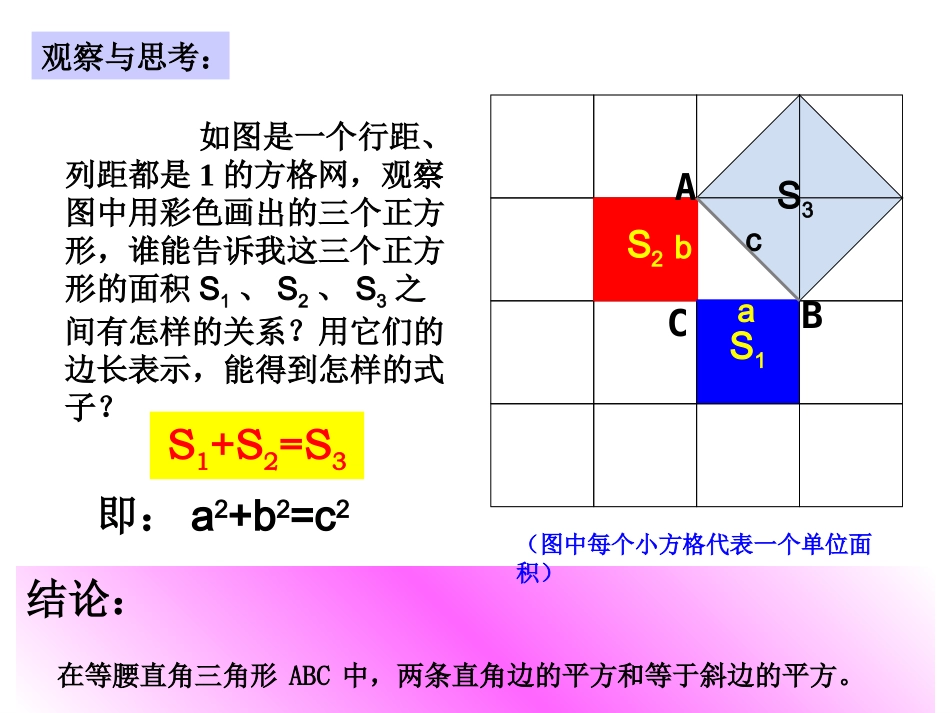
2002年世界数学大会会标18.118.1勾股定理勾股定理(第一课时)如图,受台风影响,一棵树在离地面5米处断裂,树的顶部落在离树的底部12米处,这棵树折断前有多高?y=0创设问题情境5米12米?如图是一个行距、列距都是1的方格网,观察图中用彩色画出的三个正方形,谁能告诉我这三个正方形的面积S1、S2、S3之间有怎样的关系?用它们的边长表示,能得到怎样的式子?结论:在等腰直角三角形ABC中,两条直角边的平方和等于斜边的平方。观察与思考:S2S1S3abc(图中每个小方格代表一个单位面积)ACBS1+S2=S3即:a2+b2=c2S2S1S3(图中每个小方格代表一个单位面积)图18-2S1+S2=S3,即:a2+b2=c2图18-3ABCabcACBS2S1S3观察左边图18-2、图18-3完成下表:图形S1S2S3关系图18-2图18-3991891625观察上表,你还能得到刚才的结论吗?S1+S2=S3S1+S2=S3勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么:即:直角三角形两直角边的平方和等于斜边的平方。abc师生归纳:222.abc除了上述方法可以证明勾股定理外,还有其它方法吗?继续探究caba伽菲尔德总统证法:毕达哥拉斯定理:毕达哥拉斯在国外,尤其在西方这个重要定理被称为“毕达哥拉斯定理”或“百牛定理”.相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。他发现这个定理后异常高兴,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此又叫做“百牛定理”.毕达哥拉斯(毕达哥拉斯,前572~前497),西方理性数学创始人,古希腊数学家,他是公元前五世纪的人,比周朝数学家商高晚出生五百多年.勾股知识勾股知识早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中,以后人们就简单地把这个事实说成“勾三股四弦五”,所以在我国人们就把这个定理叫作“商高定理”。商高定理就是勾股定理哦!勾股在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此,我们称上述结论为勾股定理。比一比看看谁算得快!1.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125x=15=12=13如图,受台风影响,一棵树在离地面5米处断裂,树的顶部落在离树的底部12米处,这棵树折断前有多高?5米12米?例1已知:如图18-4,在RtABC△中,两直角边AC=5,BC=12。求斜边上的高CD的长。解:在RtABC△中,22222ABACBC512169AB16913又∵在RtABC△中,ABC11SACBCABCD22,ACBC51260CD.AB1313DACB例2、已知:在Rt△ABC中,∠C=90°,CD⊥AB于D,∠A=60°,CD=,求线段AB的长.3ACBD11这节课你学到了什么知识?这节课你学到了什么知识?小结:小结:22、你还有什么疑惑或者没有弄懂的地方?课后与、你还有什么疑惑或者没有弄懂的地方?课后与同伴相互交流。同伴相互交流。作业:课堂作业:P57习题18.1第2、3、4三题。思考题:若一个直角三角形的三边长分别为3,4,x,则x=.