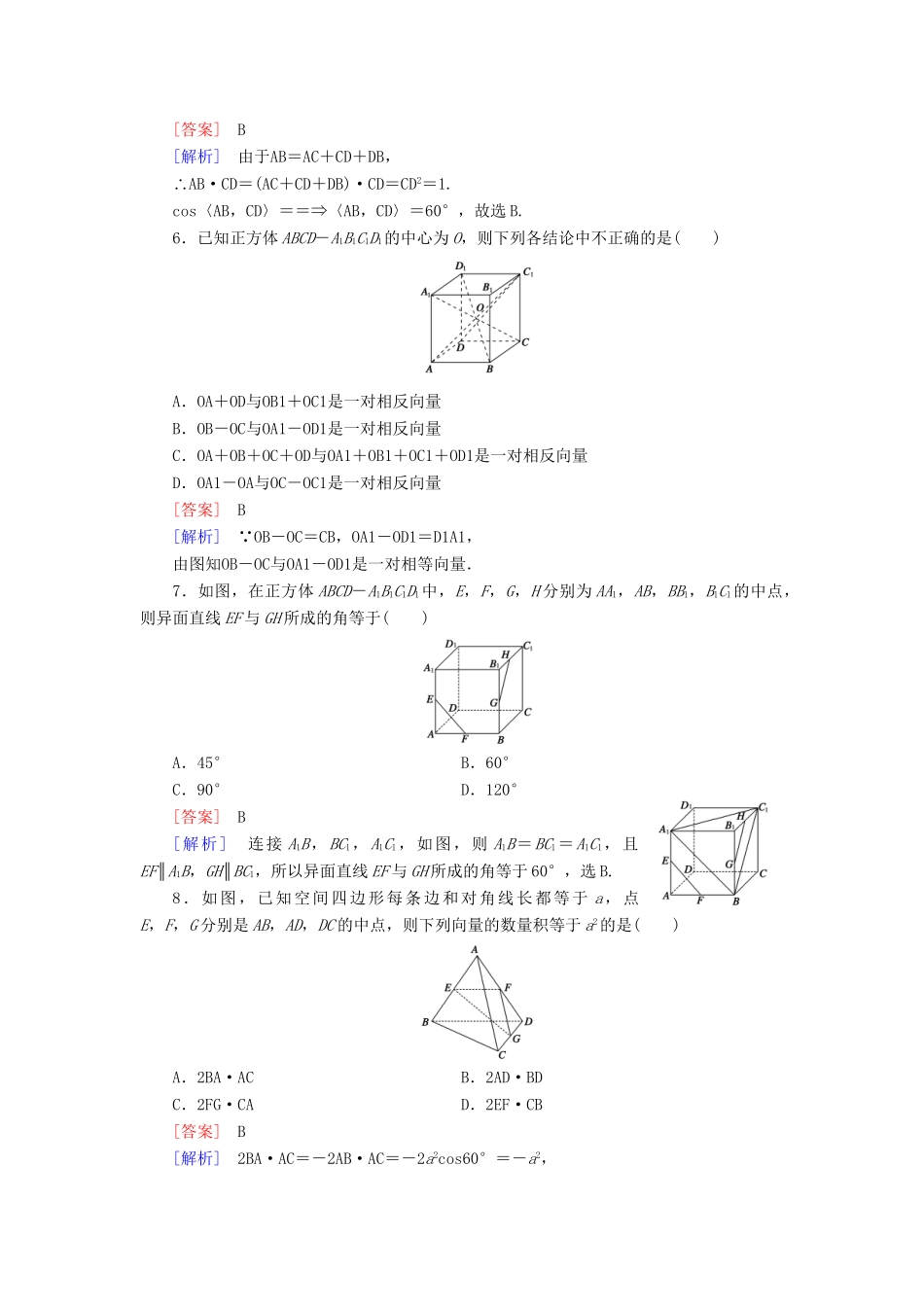
【成才之路】-学年高中数学第2章空间向量与立体几何检测题A北师大版选修2-1时间120分钟,满分150分。一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列说法中不正确的是()A.平面α的法向量垂直于与平面α共面的所有向量B.一个平面的所有法向量互相平行C.如果两个平面的法向量垂直,那么这两个平面也垂直D.如果a、b与平面α共面且n⊥a,n⊥b,那么n就是平面α的一个法向量[答案]D[解析]只有当a、b不共线且a∥α,b∥α时,D才正确.2.已知A(2,-4,-1),B(-1,5,1),C(3,-4,1),令a=CA,b=CB,则a+b对应的点为()A.(5,-9,2)B.(-5,9,-2)C.(5,9,-2)D.(5,-9,-2)[答案]B[解析]CA=(-1,0,-2),CB=(-4,9,0),故a+b=CA+CB=(-5,9,-2).3.已知a=(cosα,1,sinα),b=(sinα,1,cosα),且a∥b则向量a+b与a-b的夹角是()A.90°B.60°C.30°D.0°[答案]A[解析] |a|2=2,|b|2=2,(a+b)·(a-b)=|a|2-|b|2=0,∴(a+b)⊥(a-b).4.已知a=(λ+1,0,2),b=(6,2μ-1,2λ),若a∥b,则λ与μ的值可以是()A.2,B.-,C.-3,2D.2,2[答案]A[解析]因为a∥b,所以存在实数k,使b=ka,即(6,2μ-1,2λ)=(kλ+k,0,2k).所以所以或故选A.5.(·清华附中月考)已知a,b是两异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b且AB=2,CD=1,则直线a,b所成的角为()A.30°B.60°C.90°D.45°[答案]B[解析]由于AB=AC+CD+DB,∴AB·CD=(AC+CD+DB)·CD=CD2=1.cos〈AB,CD〉==⇒〈AB,CD〉=60°,故选B.6.已知正方体ABCD-A1B1C1D1的中心为O,则下列各结论中不正确的是()A.OA+OD与OB1+OC1是一对相反向量B.OB-OC与OA1-OD1是一对相反向量C.OA+OB+OC+OD与OA1+OB1+OC1+OD1是一对相反向量D.OA1-OA与OC-OC1是一对相反向量[答案]B[解析] OB-OC=CB,OA1-OD1=D1A1,由图知OB-OC与OA1-OD1是一对相等向量.7.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于()A.45°B.60°C.90°D.120°[答案]B[解析]连接A1B,BC1,A1C1,如图,则A1B=BC1=A1C1,且EF∥A1B,GH∥BC1,所以异面直线EF与GH所成的角等于60°,选B.8.如图,已知空间四边形每条边和对角线长都等于a,点E,F,G分别是AB,AD,DC的中点,则下列向量的数量积等于a2的是()A.2BA·ACB.2AD·BDC.2FG·CAD.2EF·CB[答案]B[解析]2BA·AC=-2AB·AC=-2a2cos60°=-a2,2AD·BD=2DA·DB=2a2cos60°=a2,2FG·CA=AC·CA=-a2,2EF·CB=BD·CB=-BD·BC=-a2.9.正方形ABCD所在平面外一点P,PA⊥平面ABCD,若PA=AB,则平面PAB与平面PCD所成的角的度数为()A.30°B.45°C.60°D.90°[答案]B[解析]以AB、AD、AP分别为x轴、y轴、z轴建立空间直角坐标系,设PA=1,则D(0,1,0),C(1,1,0),P(0,0,1),PD=(0,1,-1),CD=(-1,0,0),设平面PCD的法向量n=(x,y,z),由,得,∴,令z=1,则n=(0,1,1),显然平面PAB的一个法向量e=(0,1,0),cos〈n,e〉==,∴〈n,e〉=45°,∴二面角大小为45°.10.如下图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1.M在EF上,且AM∥平面BDE.则M点的坐标为()A.(1,1,1)B.C.D.[答案]C[解析] M在EF上,设ME=x,∴M, A(,,0),D(,0,0),E(0,0,1),B(0,,0),∴ED=(,0,-1),EB=(0,,-1),AM=.设平面BDE的法向量n=(a,b,c),由,得.故可取一个法向量n=(1,1,),有n·AM=0,∴x=1,∴M,故选C.二、填空题(本大题共5小题,每小题5分,共25分)11.已知向量a=(-1,2,3),b=(1,1,1),则向量a在b上的投影为________.[答案][解析]向量a在b上的投影为==.12.已知A(1,2,0),B(0,1,-1),P是x轴上的动点,当AP·BP取最小值时,点P的坐标为________.[答案](,0,0)[解析]设P(x,0,0),则AP=(x-1,-2,0),BP=(x,-1,1),AP·BP=x(x-1)+2=(x-)2+,∴当x=时,AP·BP取最小值,此时点P的坐标为(,0,0).13.已知空间三点A(1,1,1)、B(-1,0,4)、C(2,-2,3),...