解直角三角形VIP免费

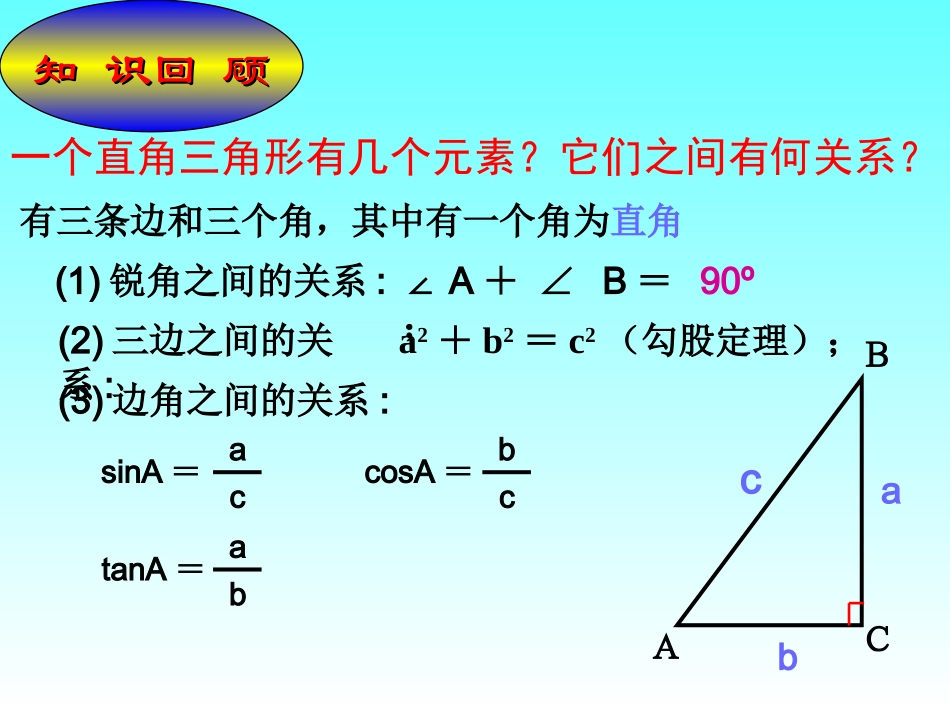
知识回顾知识回顾一个直角三角形有几个元素？它们之间有何关系？(2)三边之间的关系:a2＋b2＝c2（勾股定理）；(1)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:sinA＝accosA＝tanA＝ＡＣＢabc有三条边和三个角，其中有一个角为直角bcab30°45°60°sinαcosαtanα角α三角函数2122222132323133填一填记一记在RtABC△中,（1）根据∠A=60°,斜边AB=30,A在直角三角形的六个元素中,除直角外,如果知道两个元素,就可以求出其余三个元素.(其中至少有一个是边),想一想想一想你发现了什么BC∠BACBC6∠A∠BAB一角一边两边2（2）根据AC=，BC=你能求出这个三角形的其他元素吗？26两角（3）根∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗?不能你能求出这个三角形的其他元素吗?在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形.解直角三角形的依据:ＡＣＢabc(2)三边之间的关系:a2＋b2＝c2（勾股定理）；(1)锐角之间的关系:∠A＋∠B＝90º；(3)边角之间的关系:tanA＝absinA＝accosA＝bc归纳归纳（4）面积公式：hcbaSABC2121▲例1.如图所示，一棵大树在一次强烈的地震中于离地面5米处折断倒下，树顶落在离树根12米处.大树在折断之前高多少？解：13＋5＝18（米）.利用勾股定理可以求出折断倒下部分的长度为:1312522答:大树在折断之前高为18米.知两边5m12m练习1：在电线杆离地面8米高的地方向地面拉一条长10米的缆绳，问这条缆绳应固定在距离电线杆底部多远的地方？8米10米?BCA例2：如图，在相距2000米的东、西两炮台A、B处同时发现入侵敌舰C，在炮台A处测得敌舰C在它的南偏东400的方向，炮台B处测得敌舰C在它的正南方，试求敌舰与两炮台的距离。（精确到1米）本题本题是已是已知一知一边边,,一锐一锐角角..解：在Rt△ABC中， ∠CAB＝90゜－∠DAC＝50゜，CABABBCtan∴BC＝AB•tan∠CAB=2000×tan50゜≈2384(米).答：敌舰与A、B两炮台的距离分别约为3111米和2384米.ACAB050cosAC050cosAB050cos2000（米）。3111tan50°≈1.19175359cos50°≈0.64278760在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.例3如图，为了测量旗杆的高度BC，在离旗杆底部10米的A处，用高1.50米的测角仪DA侧得旗杆顶端C的仰角α=52°.求旗杆BC的高.（精确到0.1米）解：在Rt△CDE中，CE=DE×tanα=AB×tanα=10×tan52°≈12.80.BC=BE+CE=DA+CE≈1.50+12.80=14.3.答：旗杆BC的高度约为14.3米.ABDEC10米tan52°≈1.27994特别说明：1、在解直角三角形的过程中，常会遇到近似计算，除特别说明外，本教科书中的角度都精确到1′.2、解直角三角形，只有下面两种情况：(1)已知两条边；(2)已知一条边和一个锐角。因为根据三角形全等的判定，由于已知一个角是直角，所以在这两种情况下，对应的直角三角形唯一确定。因此，可以求出其他元素。为什么？1、在下列直角三角形中不能求解的是（）A、已知一直角边一锐角B、已知一斜边一锐角C、已知两边D、已知两角D考一考考一考1、在电线杆离地面8米高处向地面拉一条缆绳，缆绳和地面成5307′角，求该缆绳的长及缆绳地面固定点到电线杆底部的距离。（精确到0.1米）P113练习5307′8米？？ABCBCABCtan 解：（米）0.6'753tan8CtanABBCACABCsin （米）0.10'753sin8CsinABACP113练习2、海船以32.6海里\时的速度向正北方向航行，在A处看灯塔Q在海船的北偏东300处，半小时后航行到B处，发现此时灯塔Q与海船的距离最短。求灯塔Q到B处的距离。（画出图形后计算，精确到0.1海里）BQA216.32300?ABBQAtan 解：（米）4.930tan3.16AtanABBQ1.如图：某飞机在空中A处探测到它的正下方地平面上目标C，此时飞机飞行高度AC＝1200m，从飞机上看地平面指挥台B的俯角α＝16°31'，求飞机A与指挥台B的距离。（精确到1米）α 又 解：BABACBsin（米）α4221'3116sin1200sinACAB2.两座建筑物DA与B，其地面距离DC为50.4米，从DA的顶点A测得CB顶部B的仰角α=20°，测得其底部C的俯角β=35°求这两座建筑物的高（精确到0.1米）米解：...