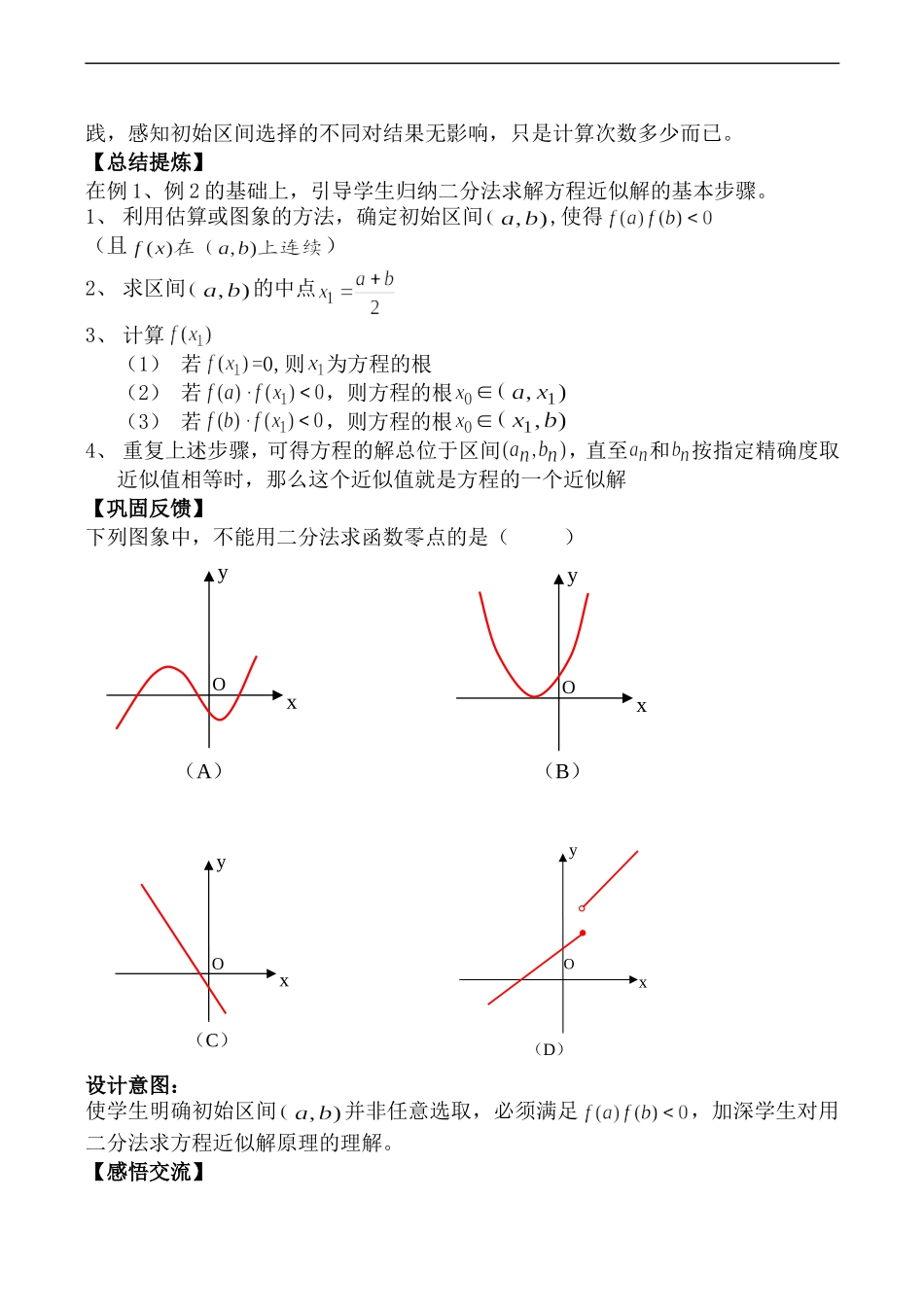
高二数学用二分法求方程的近似解教学目标:1、知识目标:理解用二分法求方程近似解的原理;能够借助计算器用二分法求方程的近似解。2、能力目标:体验并理解函数与方程的相互转化的数学思想方法;在学习过程中,让学生感受近似、逼近的思想方法;培养学生利用信息技术和计算工具的能力。3、情感目标:培养学生探究问题的能力、严谨的科学态度和创新能力;让学生在自我解决问题的过程中,体验成功的喜悦。教学重点:能够借助计算器用二分法求方程的近似解。教学难点:方程近似解所在初始区间的确定。教学过程:一、【游戏引入】同学们,现在是幸运52现场直播,下面进行一个猜数字游戏:给定1~100这100个自然数,计算机随机出一个1~100之间的整数,通过操作键盘让同学们去猜这个数,对于大家每次猜测的结果,计算机的提示是“对了”或“大了”或“小了”。【讨论】1、任给一个1~100的整数,我都可以在7次以内猜出,你们能做到吗?2、为什么采用正确的方法,7次以内一定可以猜中?(第一次猜50,若“大了”,则猜1与50中间的整数25,依次类推,由于每猜一次,就排除一半,范围不断缩小,7次以内一定可以猜中。)上述游戏,每次都将所给区间一分为二,进行比较后得到新的区间,再一分为二,如此下去,使得所猜数字逐步逼近计算机所给的数字。这种思想就是二分法。设计意图:通过做游戏,来提高学生的学习兴趣,让他们在玩的过程中初步体会二分法的思想【感受领悟】在刚才的游戏中,我们体会到了二分法的用处,你还能列举一些二分法在实际生活中的应用吗?如:翻字典查英语单词(类似二分法);输电线路的故障检测(如:一条电缆上有15个接点,现某一接点发生故障,如何可以尽快找到故障接点?)设计意图:通过列举实例,让学生进一步领悟二分法的思想,并感受到数学与生活的密切联系二、【揭示课题】我们体会到了二分法在实际生活中的用处,其实它在数学中也有很大的用处。如:类似的方程,我们现在不会解。但是,学习了二分法,我们就可以来求它的近似解。下面让我们一起来体验一下如何用二分法来求方程的近似解。三、【实践探究】例1、①判断方程在区间(0,1)内是否有解?若有,有几解?(利用两个端点的函数值异号得到在(0,1)内至少有一解;解的个数就是函数与图象交点的个数,作出两者图象,知只有一解。)②这个实数解大概是多少?你能利用二分法来解决这个问题吗?让学生展示自己的解决策略。(师生共同得出前三次,下面请学生再操作5步,2人一组互相配合,一人按计算器,一人记录过程)借助几何画板来显示这个实数解的范围逐步缩小的过程。记,设方程的实数解为,∈(0,1)第一次:∈(0,0.5)第二次:∈(0.25,0.5)第三次:∈(0.25,0.375)第四次:∈(0.3125,0.375)第五次:∈(0.3125,0.34375)第六次:∈(0.3125,0.328125)第七次:∈(0.3203125,0.328125)第八次:∈(0.3203125,0.32421875)【讨论】若精确到0.1,算几次就可以了?若精确到0.01呢?(第5次,两个端点精确到0.1的近似值都为0.3,故0.3;第8次,两个端点精确到0.01的近似值都为0.32,故0.32;)设计意图:第①题,学生容易联想到用上节课函数与方程的知识解决,目的在于分解难点,为第②题作铺垫;第②题初始区间已给定,目的在于让学生在动手操作中来体验用二分法求方程近似解的具体过程,在讨论中自我感悟运用二分法解题到底何时结束?例2、利用计算器,求方程的近似解(精确到0.1)设计意图:1、例1是初始区间已给定,而例2是初始区间未给定,需要自己找,这是一个质的变化。通过学生自主探究,来体会、归纳出确定初始区间的一般方法:估算或利用图象(函数与方程的思想)。(估算:由方程有意义及左右两边相等,可知∈(0,3);作图:考察函数与图象交点的横坐标,可知∈(2,3))2、把学生分成两组,分别就初始区间为(0,3)和(2,3)进行求解。通过学生亲自实践,感知初始区间选择的不同对结果无影响,只是计算次数多少而已。【总结提炼】在例1、例2的基础上,引导学生归纳二分法求解方程近似解的基本步骤。1、利用估算或图象的方法,确定初始区间,使得(且)2、求区间的中点3、计算(1)若=0,则为方程的根(...