高中数学第三章第三课时312 瞬时速度与瞬时加速度课件苏教版选修1-1 课件VIP免费

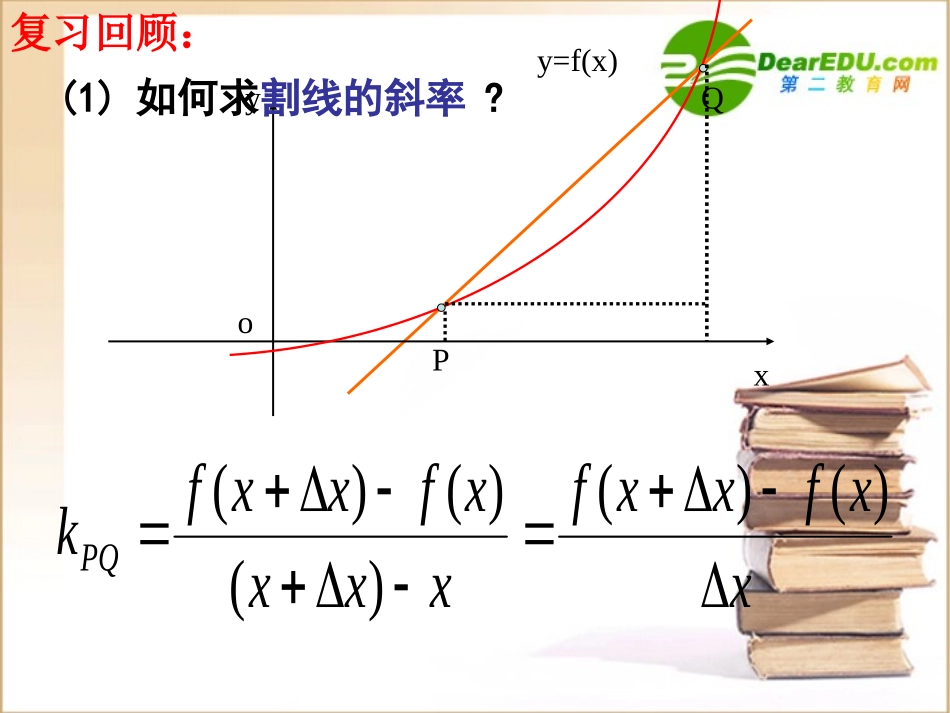
3.1.23.1.2瞬时变化率瞬时变化率－导数－导数瞬时速度和瞬时加速度PQoxyy=f(x)(1)如何求割线的斜率?xxfxxfxxxxfxxfkPQ)()()()()(复习回顾：PQoxyy=f(x)割线切线T(2)如何求切线的斜率?)斜率无限P趋限趋近点处切,时0无限趋限当(PQkxxxfxxfkPQ)()(1、先利用直线斜率的定义求出割线线的斜率；2.求出当△x趋近于0时切线的斜率3、然后利用点斜式求切线方程.求曲线在某点处的切线方程的基本步骤:平均速度：物体的运动位移与所用时间的比称为平均速度。平均速度反映物体在某一段时间段内运动的快慢程度。那么如何刻画物体在某一时刻运动的快慢程度？问题情境1：问题情境2：跳水问题.gsp跳水运动员从10m高跳台腾空到入水的过程中，不同时刻的速度是不同的。假设t秒后运动员相对于水面的高度为H(t)=-4.9t2+6.5t+10,试确定t=2s时运动员的速度。(1)计算运动员在2s到2.1s(t[2,2.1])∈内的平均速度。)/(59.1321.2)2()1.2(smHHv(2)计算运动员在2s到2+ts(t[2,2+t])⊿∈⊿内的平均速度。时间区间△t平均速度[2，2.1]0.1-13.59[2,2.01]0.01-13.149[2,2.001]0.001-13.1049[2,2.0001]0.0001-13.10049[2,2.00001]0.00001-13.100049[2,2.000001]0.000001-13.1000049当△t→0时，1.13v该常数可作为运动员在2s时的瞬时速度。设物体作直线运动所经过的路程为s=f(t)。以t0为起始时刻，物体在t时间内的平均速度为vttfttfts)()(00。就就就就就t0就就的瞬时速度，即v可作为物体在t0时刻的速度的近似值，t越小，近似的程度就越好。所以当t0时，比值vttfttfts)()(00。（瞬时速度）构建数学：ts时当的瞬时速度在0)()(000tttfttftv例1：设一辆轿车在公路上做加速直线运动，假设ts时的速度为v(t)=t2+3,（1）求t=3s时轿车的加速度；（2）求t=t0s时轿车的加速度。练习P641、2