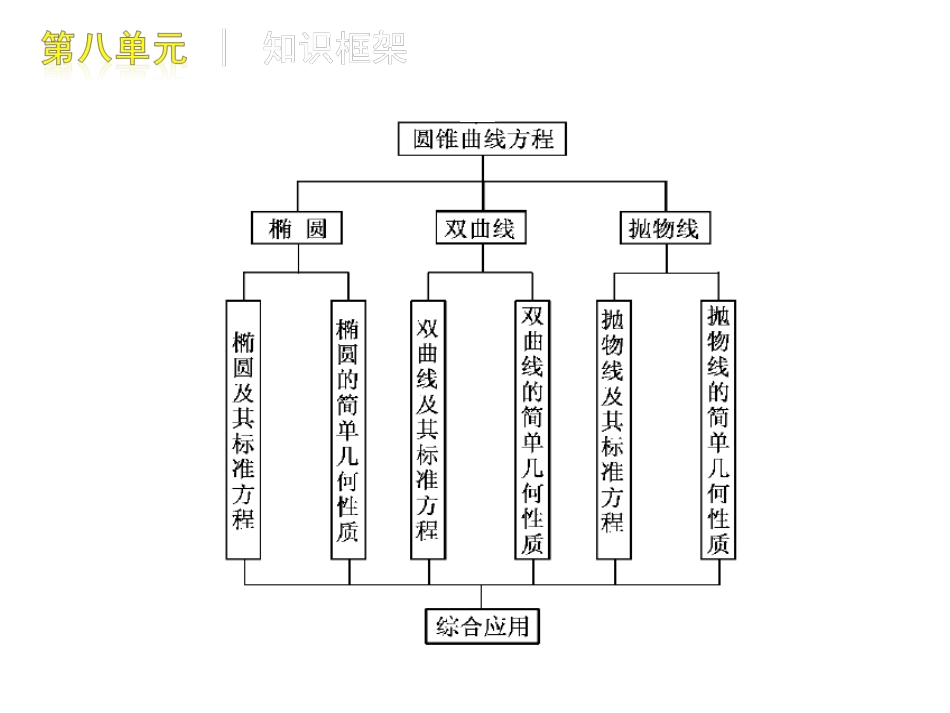
知识框架1.直线与方程(1)在平面直角坐标系中,结合具体图形,确定直线位置的几何要素.(2)理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.(3)能根据两条直线的斜率判定这两条直线平行或垂直.考纲要求(4)掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.(5)能用解方程组的方法求两条相交直线的交点坐标.(6)掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.2.圆与方程(1)掌握确定圆的几何要素,掌握圆的标准方程与一般方程.(2)能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系.(3)能用直线和圆的方程解决一些简单的问题.(4)初步了解用代数方法处理几何问题的思想.3.空间直角坐标系(1)了解空间直角坐标系,会用空间直角坐标表示点的位置.(2)会推导空间两点间的距离公式.4.圆锥曲线(1)了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用.(2)掌握椭圆的定义、几何图形、标准方程及简单几何性质.(3)了解双曲线、抛物线的定义、几何图形和标准方程,知道它们的简单几何性质.(4)理解数形结合的思想.(5)了解圆锥曲线的简单应用.1.该部分的主要考查点是直线与圆的方程、圆锥曲线与方程,在试卷中一般是两个小题,重点考查直线与圆、圆锥曲线的基础知识与方法;一个解答题,重点考查解析几何的基本思想方法,一般是以圆锥曲线(特别是椭圆)为依托进行考查,在考试大纲降低了对圆锥曲线要求后,也不排除以圆为依托命制综合解答题的可能.命题趋势2.预计2011年该部分的考查会延续近年来的传统,命制两个小题,一个考查直线与圆,一个考查圆锥曲线的基础知识(一般是双曲线或抛物线);一个大题,以圆锥曲线为载体考查解析几何的基本思想和方法.1.本单元内容是解析几何的核心内容,包括直线、圆与圆锥曲线三个部分,是高考灵活考查基础知识和运用能力的载体.本单元内容集中体现了用坐标法研究曲线的思想方法.概念、公式较多,且有一定的综合性.本单元的重点是直线、圆与简单的圆锥曲线的基本性质;难点是直线与圆锥曲线的综合应用问题,此部分思维量相对较大,运算较为复杂,方法灵活多样,是考查学生综合能力的必考内容.使用建议2.复习过程中建议重点关注以下几个问题:(1)对于曲线的方程和方程的曲线要求掌握基本的求曲线方程的方法,比如相关点代入法、定义法等,这常常是解答题第一小问的命题点;(2)重视数学思想方法的应用分类讨论思想、数形结合思想、转化与思想、函数与方程思想以及解析法、待定系数法等在各种题型中均有体现.圆锥曲线问题的解答过程计算量较大,对运算能力要求较高,寻求简捷合理的运算途径显得尤为重要.常用的减负途径有:设而不求、活用定义、妙用平面几何性质、根与系数的关系、统一方程、巧用对称等.(3)发挥向量的工具作用平面向量与圆锥曲线都涉及坐标表示和坐标运算,坐标法可以将两者有机结合起来,使向量的有关运算与圆锥曲线的坐标运算产生了有机联系,形成了新的知识交汇点,这既给圆锥曲线的命题提供了新的思路,也为解答圆锥曲线问题提供了新的工具,复习时切不可忽视.(4)适度关注平面几何的性质圆锥曲线研究的对象毕竟是几何图形,所以应重视发挥平面几何有关性质在圆锥曲线中的应用,特别应重视平面几何重要定理的深化和推广以及射影几何某些性质特殊化可能成为圆锥曲线为命题的新的命题点.3.本单元课时安排如下:本单元共8讲,其中第48讲安排2课时,其余各讲各1课时,再加1个45分钟滚动基础训练卷和1个45分钟单元能力训练卷,各用1个课时,共需11课时.