高中数学(直线的方向向量)课件VIP免费

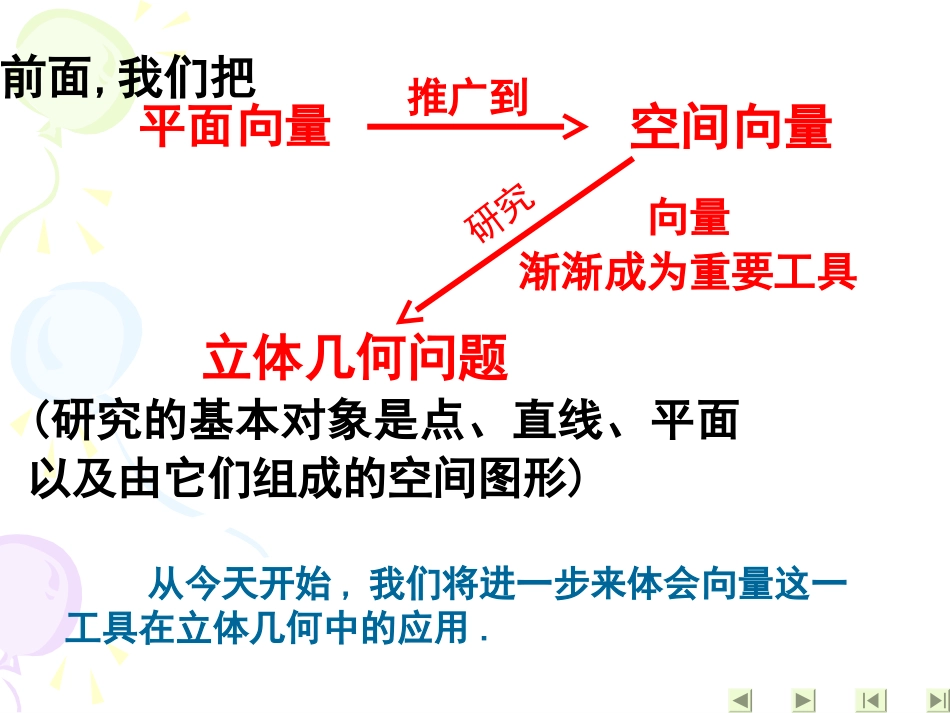
直线的方向向量复习、向量的直角坐标运算的几个公式.111222(,,),(,,)axyzbxyz设则1212120;abxxyyzzab//ab121212,,()xxyyzzR121212222222111222cos,xxyyzzabababxyzxyz平面向量空间向量推广到立体几何问题(研究的基本对象是点、直线、平面以及由它们组成的空间图形)向量渐渐成为重要工具研究从今天开始,我们将进一步来体会向量这一工具在立体几何中的应用.前面,我们把问：1、如何用向量来表示直线的位置关系？2、直线的方向向量定义：3、两条直线所成的角与两直线方向向量所成的角的关系,ab练习1、设直线,lm的方向向量分别为,ab，根据下列条件判断直线所成的角,lm1)(2,3,1),(6,9,3)ab2)(5,0,2),(0,4,0)ab3)(2,2,0),(1,0,1)ab两直线l,m所成的角为(02≤≤),cosabab；例2、如图在边长为1的正方体ABCD-A1B1C1D1中，E、F分别是C1B1、D1C1、的中点，求AD1与EF所成的角zxyABCDA1B1C1D1EF练习1、P117练习2用两种方法：一：选基底的方法二：用坐标的方法并对两种方法进行比较例3、若一非平面四边形对边长相等，证明两对角线中点连线垂直于两对角线DCABNM提示：先翻译成数学语言设直线,lm的方向向量分别为,ab，两直线l,m所成的角为(02≤≤),cosabab；课堂小结：用空间向量解决立体几何问题的“三步曲”。（1）建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线、平面，把立体几何问题转化为向量问题；（2）通过向量运算，研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题；（3）把向量的运算结果“翻译”成相应的几何意义。（化为向量问题）（进行向量运算）（回到图形问题）