高中数学 向量数量积的运算律课件 新人教B版必修4 课件VIP免费

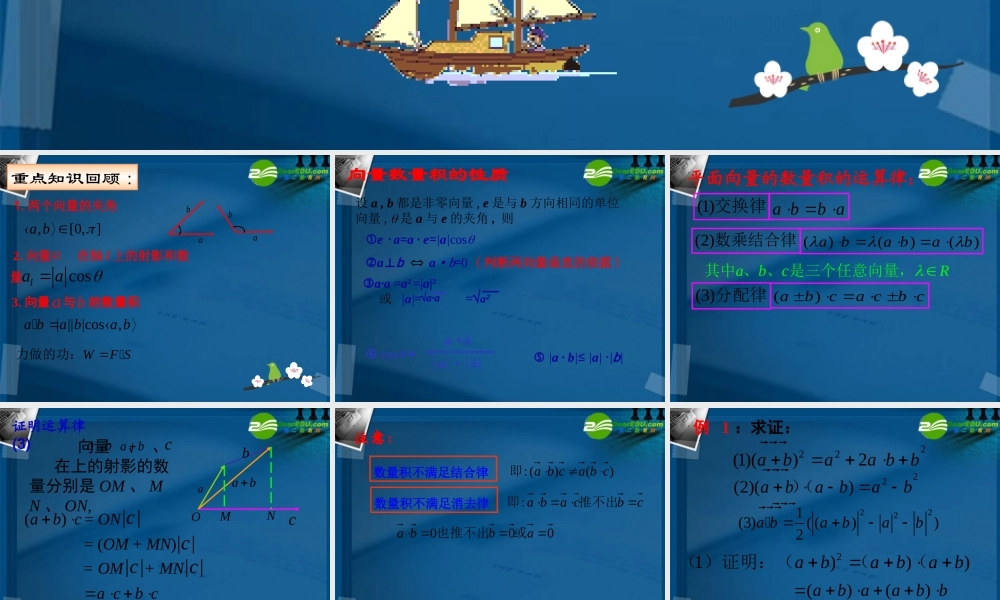
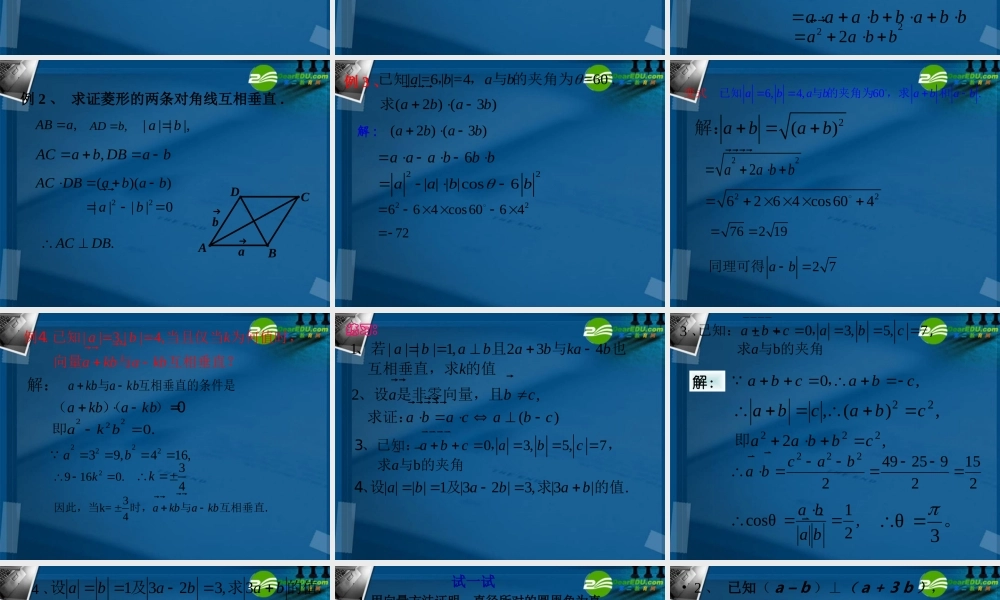
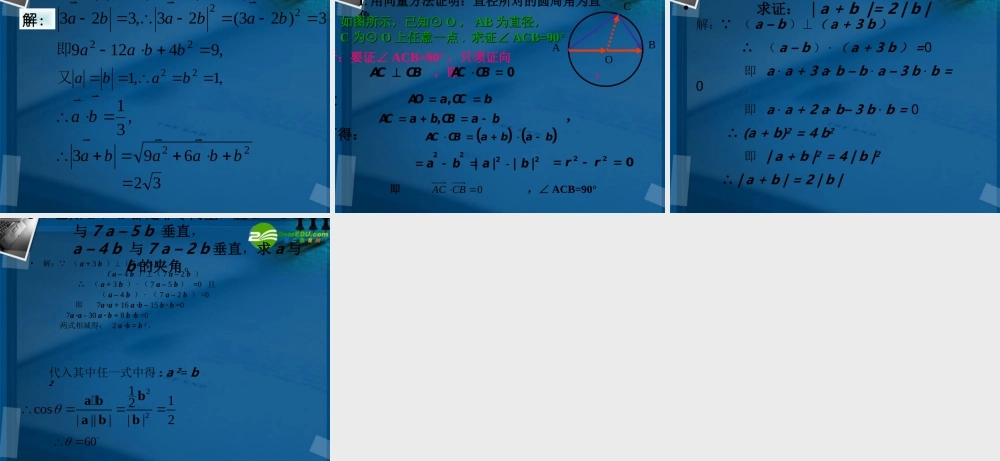
§2.3.2 向量数量积的运算律1. 两个向量的夹角abab,[0, ]a b3. 向量 与 的数量积ab| || |cos,a ba ba b 2. 向量 在轴 l 上的射影和数量acoslaa 重点知识回顾 :WF S力做的功：向量数量积的性质 设 a , b 都是非零向量 , e 是与 b 方向相同的单位向量 ,  是 a 与 e 的夹角 , 则 e · a=a · e=|a|cos a⊥b a·b=0 ( 判断两向量垂直的依据 )  |a · b|≤ |a| ·|b| a·a =a2 =|a|2 或 |a|= =√a·a√a2 cos = a·b |a|·|b|平面向量的数量积的运算律：(1)交换律abcR 其中 、 、 是三个任意向量，()()()aba bab  (3)分配律a bb a  (2)数乘结合律()abca cb c    ONM证明运算律(3)ababcababc 向量 、 、 在上的射影的数量分别是 OM 、 MN 、 ON, = ON ()abc| |ca cb c    = (OM + MN) | |c| |c| |c= OM + MN注意：数量积不满足结合律)()(:cbacba即数量积不满足消去律cbcaba推不出即:000abba或也推不出例 1 ：求证：222(1)()2abaa bb 22(2)()ababab）（21)))ababab（ ）证明：（（（()()abaabb a aa bb ab b      222aa bb 2221(3)( ())2a babab例 2 、 求证菱形的两条对角线互相垂直 . baDCBA,ABa�,ADb�,ACab DBab  �|| ||,ab22()() ||||0AC DBab abab�.ACDB�例 3 、解 :(2 ) (3 )abab6a aa bb b   22| | | |cos6aabb��2266 4 cos606 4 72| |=6 | |=4=60 .(2 ) (3 )abababab已知，， 与 的夹角为求6,4,60.abababab已知与 的夹角为，求和变 式 2()abab解：222aa bb 2262 6 4 cos604   762 192 7ab...