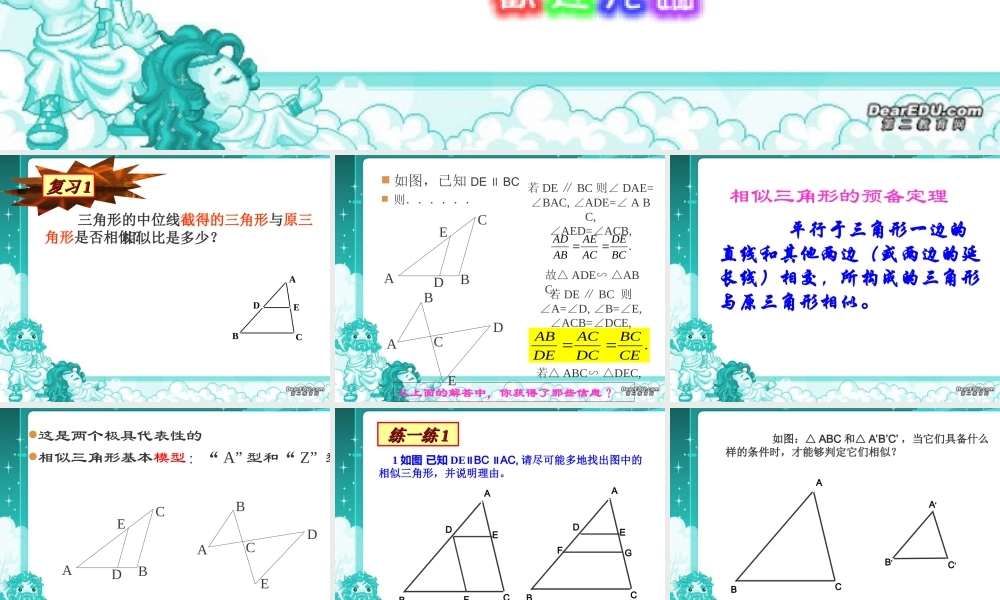
三角形的中位线截得的三角形与原三角形是否相似?相似比是多少?ABCDE复习复习 11ABDECABCDE 如图,已知 DE ∥ BC 则.......CEBCDCACDEAB若 DE ∥ BC 则∠A=D, B=E,∠∠∠∠ACB=DCE,∠故△ ADE AB∽ △C,若△ ABC DEC,∽ △从上面的解答中,你获得了那些信息?若 DE ∥ BC 则∠ DAE=BAC, ADE= A B∠∠∠C,∠AED=ACB,∠.BCDEACAEABAD 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。相似三角形的预备定理ABCDEABDEC这是两个极具代表性的相似三角形基本模型:“ A” 型和“ Z” 型这个两个模型在今后学习的过程中作用很大 ,你可要认真噢! 1 如图 已知 DE BC∥ AC,∥请尽可能多地找出图中的相似三角形,并说明理由。练一练练一练 11ABCDFEABCDFEG 如图:△ ABC 和△ A’B’C’ ,当它们具备什么样的条件时,才能够判定它们相似? ABCA'B'C'ABCA'B'C' 如图 △ ABC 和△ A'B'C' 中 , A=A', B=B’ . ∠∠∠∠ 问△ ABC 与△ A'B'C' 是否相似 ?在△ ABC 边 AB 上 , 截取 AD=A’B’, 过 D 作 DEBC∥交 AC 于 E. 则有△ ADEABC∽△ ∴△A'B'C'ABC.∽△证明CBADEA ’B ’C ’ ∠ADE=B , B=B ' ∠∠∠∴∠ADE=B ' ∠又 ∠ A=A' , AD=A ' B ' ∠∴△ADEA ' B ' C ' (ASA)≌△判定定理 1: 如果一个三角形的两个角与另一个三角形的两个角对应相等 , 那么这两个三角形相似 .证明 : 在△ ABC 中 , A=40∠°, B=80°, ∠ ∴∠C=180° - 40 ° - 80 °=60 ° 在△ DEF 中 , E=80°, F=60°.∠∠ ∴∠B=E, C=F∠∠∠ ∴△ABCDEF(∽△两个角对应相等 , 两三角形相似 ).试一试:已知 : ABC△和△ DEF 中 , A=40°, B=80°. ∠∠∠E=80°, F=60°.∠求证 : ABCDEF.△∽△ABCDEF40808060已知: Rt ABC△中,∠ ACB = 90° , CDAB⊥ 试 图中有几对相似三角形 .证明: ∠ B=B∠,∠ CDB=ACB=90°∠, ∴△ABCCDB(∽△两个角对应相等 , 两三角形相似 ). 同理可证:△ ABCACD∽△ ∴△ABCCBDACD.∽△∽△CABD 已知:如图 RtABC△中, CD 是斜边上的高。求证:△ ABCCBDACD∽△∽△小结 :判定定理 1: 如果一个三角形的两个角与另一个三角形的两个角对应相等 , 那么这两个三角形相似 .简单说成 : 两个角对应相...