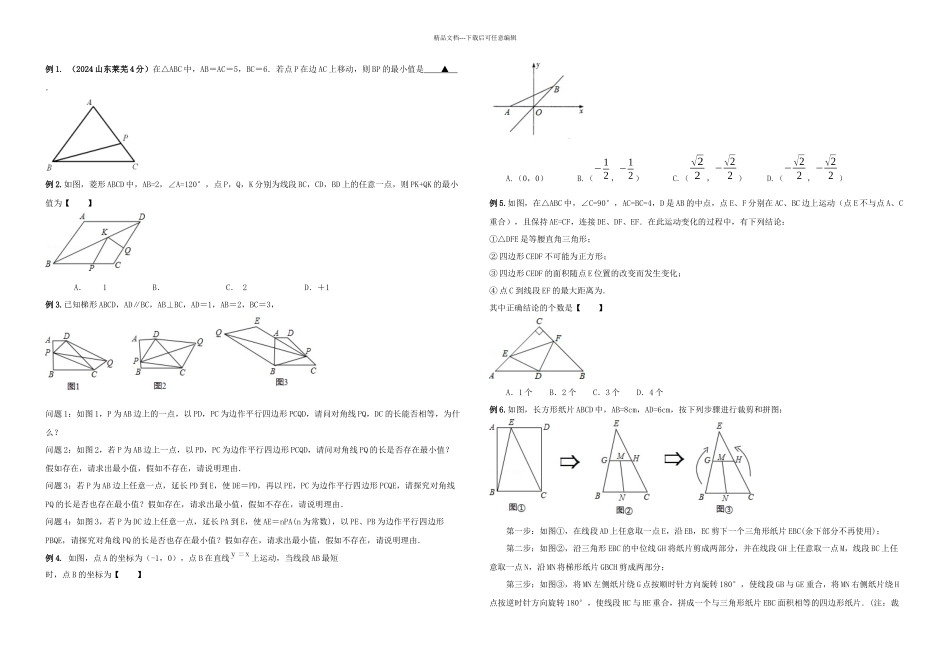
精品文档---下载后可任意编辑在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。下面通过近年全国各地中考的实例探讨其解法。应用两点间线段最短的公理(含应用三角形的三边关系)求最值典型例题:例 1. 如图,∠MON=90°,矩形 ABCD 的顶点 A、B 分别在边 OM,ON 上,当 B 在边 ON 上运动时,A 随之在边 OM 上运动,矩形 ABCD 的形状保持不变,其中 AB=2,BC=1,运动过程中,点 D 到点 O 的最大距离为【 】A. B. C.5 D.例 2.在锐角三角形 ABC 中,BC=,∠ABC=45°,BD 平分∠ABC,M、N 分别是 BD、BC 上的动点,则 CM+MN 的最小值是 ▲ 。例 3.如图,圆柱底面半径为,高为,点 A、B 分别是圆柱两底面圆周上的点,且 A、B 在同一母线上,用一棉线从 A 顺着圆柱侧面绕 3 圈到 B,求棉线最短为 ▲ 。练习题:1. 如图,长方体的底面边长分别为 2 和 4,高为 5.若一只蚂蚁从 P 点开始经过 4 个侧面爬行一圈到达 Q 点,则蚂蚁爬行的最短路径长为【 】2.如图,圆柱的底面周长为 6cm,AC 是底面圆的直径,高 BC=6cm,点 P 是母线 BC 上一点,且 PC=BC.一只蚂蚁从 A 点出发沿着圆柱体的表面爬行到点 P 的最短距离是【 】 A、㎝ B、5cm C、㎝ D、7cm3.如图所示,在边长为 2 的正三角形 ABC 中,E、F、G 分别为 AB、AC、BC 的中点,点 P 为线段 EF 上一个动点,连接 BP、GP,则△BPG 的周长的最小值是 _ ▲ .二、应用垂线段最短的性质求最值:典型例题:精品文档---下载后可任意编辑例 1. (2024 山东莱芜 4 分)在△ABC 中,AB=AC=5,BC=6.若点 P 在边 AC 上移动,则 BP 的最小值是 ▲ .例 2.如图,菱形 ABCD 中,AB=2,∠A=120°,点 P,Q,K 分别为线段 BC,CD,BD 上的任意一点,则 PK+QK 的最小值为【 】 A.1 B. C. 2 D.+1例 3.已知梯形 ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,问题 1:如图 1,P 为 AB 边上的一点,以 PD,PC 为边作平行四...