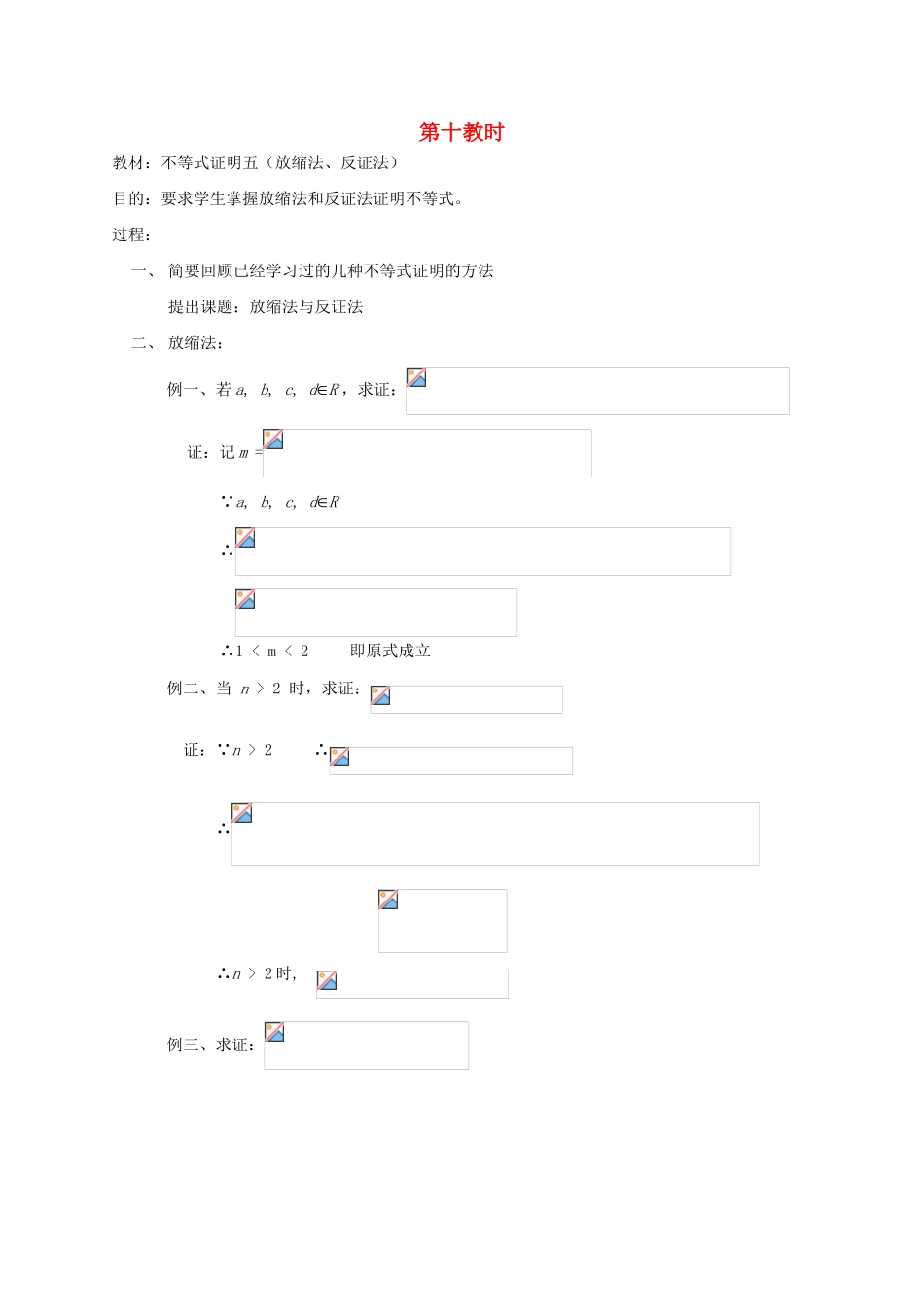
第十教时教材:不等式证明五(放缩法、反证法)目的:要求学生掌握放缩法和反证法证明不等式。过程:一、 简要回顾已经学习过的几种不等式证明的方法提出课题:放缩法与反证法二、 放缩法:例一、若 a, b, c, dR+,求证:证:记 m = ∵a, b, c, dR+ ∴ ∴1 < m < 2 即原式成立例二、当 n > 2 时,求证: 证:∵n > 2 ∴ ∴ ∴n > 2 时, 例三、求证: 证: ∴三、 反证法:例四、设 0 < a, b, c < 1,求证:(1 a)b, (1 b)c, (1 c)a,不可能同时大于 证:设(1 a)b >, (1 b)c >, (1 c)a >,则三式相乘:ab < (1 a)b•(1 b)c•(1 c)a < ①又∵0 < a, b, c < 1 ∴同理:, 以上三式相乘: (1 a)a•(1 b)b•(1 c)c≤ 与①矛盾∴原式成立例五、已知 a + b + c > 0,ab + bc + ca > 0,abc > 0,求证:a, b, c > 0 证:设 a < 0, ∵abc > 0, ∴bc < 0 又由 a + b + c > 0, 则 b + c = a > 0 ∴ab + bc + ca = a(b + c) + bc < 0 与题设矛盾 又:若 a = 0,则与 abc > 0 矛盾, ∴必有 a > 0 同理可证:b > 0, c > 0四、 作业:证明下列不等式:1. 设 x > 0, y > 0,, ,求证:a < b放缩法:2. lg9•lg11 < 1 3. 4. 若 a > b > c, 则 5.左边6. 7.已知 a, b, c > 0, 且 a2 + b2 = c2,求证:an + bn < cn (n≥3, nR*) ∵,又 a, b, c > 0, ∴ ∴8.设 0 < a, b, c < 2,求证:(2 a)c, (2 b)a, (2 c)b,不可能同时大于 1仿例四9.若 x, y > 0,且 x + y >2,则和中至少有一个小于 2反设≥2,≥2 ∵x, y > 0,可得 x + y ≤2 与 x + y >2 矛盾